HalfEdge数据结构详解
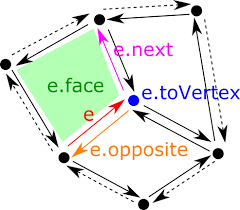
我们可以将离散表面表示为多边形网格。 多边形网格可以被认为是图(具有顶点和顶点之间的边)加上面列表,其中面是边的环。
下面,我们将网格指定为顶点列表和面列表,其中每个面都指定为顶点环。 网格的边是隐含的——边连接面的相邻顶点。
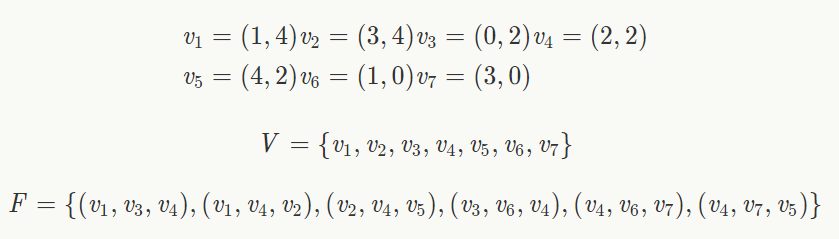
由于不含冗余信息,面列表表示在磁盘存储中很受欢迎,但是很难编写直接在这种表示上运行的算法。 例如,判断v6和v3是否连接,我们必须遍历面列表,直到找到(或找不到)我们正在寻找的边。
可以在恒定时间内回答此类查询的流行数据结构是半边( HalfEdge)数据结构。 在半边数据结构中,我们通过用一对有向半边孪生表示每条边来显式存储网格的边,两个半边孪生中的每一个都指向相反的方向。 半边存储对其孪生的引用,以及对沿同一面或孔的前一个和下一个半边的引用。 顶点存储其位置和对源自该顶点的任意半边的引用,而面存储属于该面的任意半边。 半边数据结构存储顶点、面和半边记录的数组。
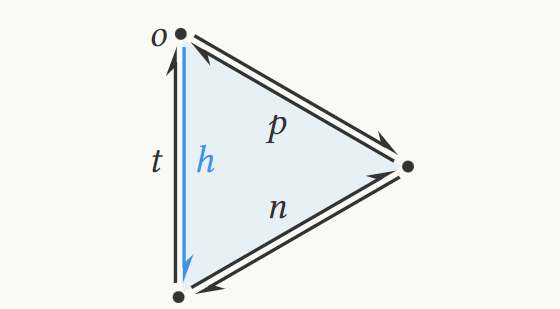
上图为半边 h 及其孪生、下一个和前一个半边的可视化。 h 还存储对其原始顶点和入射面的引用。
为了表示边界边缘(与孔相邻的边),我们有两种选择。 我们可以用双指针为空的单个半边表示边界边,或者我们可以将边界边表示为一对半边,与孔相邻的半边具有空面指针。 事实证明,后一种设计选择导致更简单的代码,因为我们很快就会看到获得半边的孪生是比获得半边的面更常见的操作,并且能够简单地假设我们有一个非空孪生导致的特殊情况要少得多。
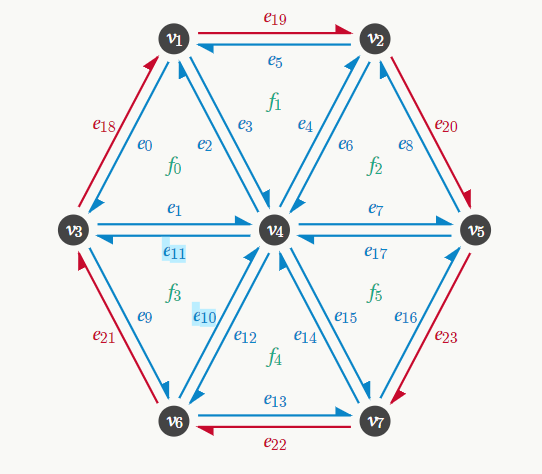
下面我们展示了一个更复杂的网格的半边图和记录表,要表示的网格如下图所示:
可以在编辑器中编辑网格顶点和连接:
# Enter your mesh definition in OBJ format below...
v 1.0 4.0 0.0
v 3.0 4.0 0.0
v 0.0 2.0 0.0
v 2.0 2.0 0.0
v 4.0 2.0 0.0
v 1.0 0.0 0.0
v 3.0 0.0 0.0
f 1 3 4
f 1 4 2
f 2 4 5
f 3 6 4
f 4 6 7
f 4 7 5对应的记录如下:
| Vertex | Coordinate | Incident edge |
|---|---|---|
| v1 | (1, 4, 0) | e0 |
| v2 | (3, 4, 0) | e5 |
| v3 | (0, 2, 0) | e1 |
| v4 | (2, 2, 0) | e2 |
| v5 | (4, 2, 0) | e8 |
| v6 | (1, 0, 0) | e10 |
| v7 | (3, 0, 0) | e14 |
| Face | Half-edge |
|---|---|
| f0 | e0 |
| f1 | e3 |
| f2 | e6 |
| f3 | e9 |
| f4 | e12 |
| f5 | e15 |
| Half-edge | Origin | Twin | Incident face | Next | Prev |
|---|---|---|---|---|---|
| e0 | v1 | e18 | f0 | e1 | e2 |
| e1 | v3 | e11 | f0 | e2 | e0 |
| e2 | v4 | e3 | f0 | e0 | e1 |
| e3 | v1 | e2 | f1 | e4 | e5 |
| e4 | v4 | e6 | f1 | e5 | e3 |
| e5 | v2 | e19 | f1 | e3 | e4 |
| e6 | v2 | e4 | f2 | e7 | e8 |
| e7 | v4 | e17 | f2 | e8 | e6 |
| e8 | v5 | e20 | f2 | e6 | e7 |
| e9 | v3 | e21 | f3 | e10 | e11 |
| e10 | v6 | e12 | f3 | e11 | e9 |
| e11 | v4 | e1 | f3 | e9 | e10 |
| e12 | v4 | e10 | f4 | e13 | e14 |
| e13 | v6 | e22 | f4 | e14 | e12 |
| e14 | v7 | e15 | f4 | e12 | e13 |
| e15 | v4 | e14 | f5 | e16 | e17 |
| e16 | v7 | e23 | f5 | e17 | e15 |
| e17 | v5 | e7 | f5 | e15 | e16 |
| e18 | v3 | e0 | ∅ | e19 | e21 |
| e19 | v1 | e5 | ∅ | e20 | e18 |
| e20 | v2 | e8 | ∅ | e23 | e19 |
| e21 | v6 | e9 | ∅ | e18 | e22 |
| e22 | v7 | e13 | ∅ | e21 | e23 |
| e23 | v5 | e16 | ∅ | e22 | e20 |
遍历面的顶点/边
有时我们需要遍历一个面以获得它的所有顶点或半边。 例如,如果我们想计算一个面的质心,我们必须找到面的所有顶点的位置。
在代码中,给定面 f,这看起来像这样:
start_he = f.halfedge
he = start_he
do {
# do something useful
he = he.next
} while he != start_he请注意,我们使用 do-while 循环而不是 while 循环,因为我们想在循环迭代结束时检查条件。 在第一次迭代开始时, he == start_he,因此如果我们在循环开始时检查条件,我们的循环将不会运行任何迭代。
要以相反的方向遍历面,可以简单地将 he.next 替换为 he.prev。
围绕一个顶点进行遍历
前面我们描述了如何构造面迭代器。 另一个有用的迭代器是顶点迭代器。 通常,我们想要围绕一个顶点迭代顶点环(也称为顶点伞)。 更具体地说,我们想要遍历所有以给定顶点为原点的半边。
在本文中我们将假定面的顶点顺序为逆时针(这是 OpenGL 中的默认设置)。
给定顶点 v,以逆时针顺序遍历所有从 v 出来的半边,代码如下所示:
start_he = v.halfedge
he = start_he
do {
# do something useful
he = he.prev.twin
} while he != start_he请注意,即使存在边界半边或非三角形面,我们的代码仍然有效。
以顺时针顺序遍历顶点环与以逆时针顺序遍历环非常相似,只是我们将 he = he.prev.twin 替换为 he = he.twin.next。
修改半边数据结构
前面我们讨论了如何迭代面和顶点环。 修改半边数据结构比较棘手,因为如果记录修改不当,引用很容易变得不一致。
作为练习,我们将介绍如何实现 EdgeFlip 算法,给定两个三角形面中间的半边,翻转半边及其孪生的方向。
我们将在算法的每一步显示记录表。
我们从突出显示的输入半边开始(下面网格中的 e3 或 e2,但假设是 e3)。
我们首先获取所有受影响的半边的引用,因为在网格处于不一致状态时遍历网格将很困难。
def FlipEdge(HalfEdge e):
e5 = e.prev
e4 = e.next
twin = e.twin
e1 = twin.prev
e0 = twin.next接下来,我们确保没有对 e 或 twin(图中的 e3 和 e2)的面或顶点引用,我们将在执行边翻转的过程中回收它们。
for he in {e0, e1, e4, e5}:
he.origin.halfedge = &he
e1.face.halfedge = &e1
e5.face.halfedge = &e5这些操作是安全的,因为代表性半边的选择是任意的; 网格仍处于一致状态。 受影响的单元格颜色为浅蓝色,但并非所有单元格都更改为与其旧值不同的值。
接下来我们回收e和twin。 我们将(任意地)让 e 成为图中的顶部对角线半边,并且 twin 成为它的孪生。 我们可以按照下图填写e和twin的成员。 在此之后,我们的数据结构将变得不一致。 我们用红色勾勒出不一致的单元。
e.next = &e5
e.prev = &e0
e.origin = e1.origin
e.face = e5.face
twin.next = &e1
twin.prev = &e4
twin.origin = e5.origin
twin.face = e1.face我们更新受影响的下一个和上一个参考。 同样,我们可以参考图表来填写这些值。
e0.next = &e
e1.next = &e4
e4.next = &twin
e5.next = &e0
e0.prev = &e5
e1.prev = &twin
e4.prev = &e1
e5.prev = &e
原文链接:Half-Edge Data Structures
BimAnt翻译整理,转载请标明出处