IfcTransitionCode

Definition from ISO/CD 10303-42:1992: This type conveys the continuity properties of a composite curve or surface. The continuity referred to is geometric, not parametric continuity. For example, in ContSameGradient the tangent vectors of successive segments will have the same direction, but may have different magnitude.

NOTE Corresponding STEP type: transition_code, please refer to ISO/IS 10303-42:1994, p. 14 for the final definition of the formal standard.

HISTORY New Type in IFC Release 1.0

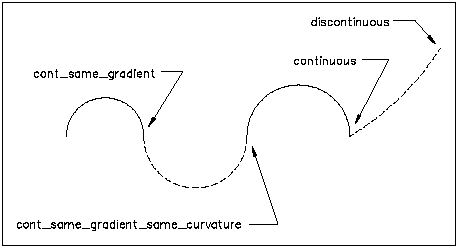
transition code

Figure quoted from ISO/CD 10303-42:1992, p. 55

ENUMERATION

Discontinuous: The segments do not join. This is permitted only at the boundary of the curve or surface to indicate that it is not closed.
Continuous: The segments join but no condition on their tangents is implied.
ContSameGradient: The segments join and their tangent vectors or tangent planes are parallel and have the same direction at the joint: equality of derivatives is not required.
ContSameGradientSameCurvature: For a curve, the segments join, their tangent vectors are parallel and in the same direction and their curvatures are equal at the joint: equality of derivatives is not required. For a surface this implies that the principle curvatures are the same and the principle directions are coincident along the common boundary.

EXPRESS specification:

TYPE IfcTransitionCode = ENUMERATION OF

(	DISCONTINUOUS, CONTINUOUS, CONTSAMEGRADIENT, CONTSAMEGRADIENTSAMECURVATURE);

END_TYPE;