NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模
那些读过我的圣诞假期更新的人会知道,我稍微绕道了低级图形和游戏编程,从头开始编写一个 C++ 体素引擎,既有趣又充满挑战。 我一直在尽可能地继续修改它,并添加了对基于体素的精灵的支持。 在下面的屏幕截图中,外星人、玩家和子弹都由体素组成,并以一种隐约让人想起经典太空入侵者游戏的方式在世界空间中移动:

尽管我意识到它看起来只是一个平面纹理网格,并且平面纹理网格的效率比体素高很多倍,但地面也是由体素组成的。
当然,一旦你添加精灵或任何移动到世界的东西,就会开始考虑检测碰撞并有效地执行此操作仍然是一个有趣的开发领域,不同的方法对于不同的条件或多或少是最佳的。 这本质上是一个空间组织问题。 因此,尽管你可能会想“呃,碰撞检测,这对我有什么用?” 不难看出类似的索引方法如何有助于回答不涉及游戏的类似问题。 同样,尽管 A* 算法传统上被认为是一种游戏算法,但我发现自己在一些非常有趣的非游戏空间中使用它。
在体素引擎中的精灵之间发生碰撞的情况下,我需要考虑数百个对象,这些对象由分布在不确定但本质上非常大且大多稀疏的三维空间中的数百万个体素组成。 每个精灵之间的像素/体素完美检测显然会非常昂贵,因此通常碰撞检测分为两个阶段:
- 大范围碰撞——快速列出可能发生碰撞的候选清单。
- 窄范围碰撞 - 使用额外的细节来过滤宽范围传递到实际像素/体素完美碰撞中可能产生的碰撞。
我在体素引擎中解决大范围问题的第一次尝试是一个常见的问题,它利用了一种有效的方法来确定两个框(2d 或 3d)是否相交,这依赖于它们的轴对齐 - 因此轴对齐的边界框, 或AABB。 如果这听起来很复杂——别担心,事实并非如此,我稍后会解释。
网上有很多这种方法的实现以及各种博客文章和教程,但我没有找到任何将它们结合在一起的内容,因此接下来是 AABB 的分步指南以及如何在树中对它们进行排序以快速确定交叉点 。 我的体素引擎中以 C++ 实现的形式提供了示例代码,在本文的底部,我解释了如何在你自己的代码中使用它(仅是 AABB 树实现)。 然而,这篇文章更多的是关于理论,一旦你了解简单的实现是相当简单的(尽管有许多优化,其中一些在我的示例代码中,另一些则不在,这可能会使事情变得复杂)。
为了使本指南保持简单,我将绘制图表并讨论 2 维框(矩形)而不是 3 维框,但是从字面上看,要添加第 3 维,只需要在第 3 维中添加即可。 无论 x 和 y 在下面适用的地方,都按照与 x 和 y 相同的模式添加 z。
1、什么是 AABB?
AABB 比听起来更简单 – 它们本质上是包围盒,与坐标轴(因此 2d 的 x,y 和 3d 的 x,y,z)沿同一方向对齐/运行。 名称的边界部分是因为当用于碰撞检测或作为树的一部分时,它们通常包含或绑定其他框。 下图显示了两个简单且兼容的 AABB:
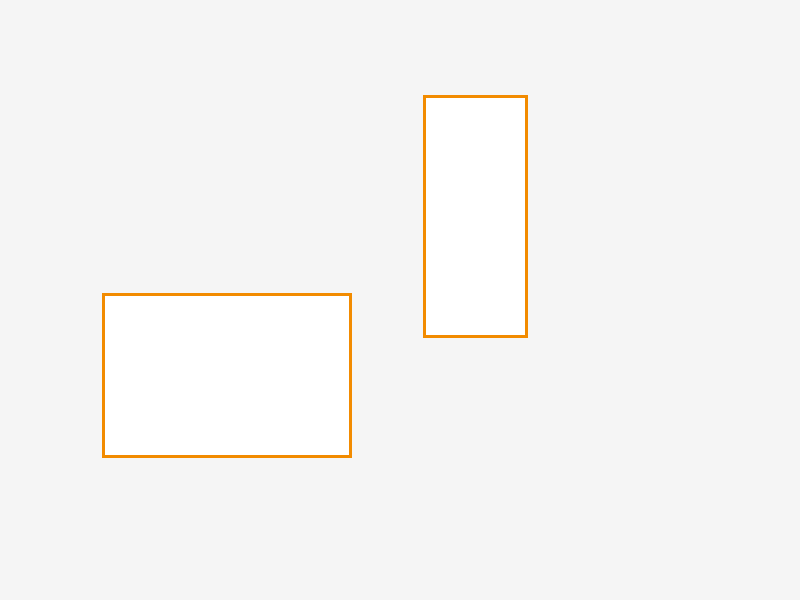
相反,下图中显示的两个框不是 AABB,因为它们与坐标轴不对齐:

AABB 的一个关键特征是它所占据的空间可以由 2 个点来定义,无论它是在 2 维空间还是 3 维空间中。 在二维空间中,两个点是 (minx, miny) 和 (maxx, maxy)。
这可用于执行非常快速的检查两个 AABB 是否相交。 考虑下图中的两个 AABB:
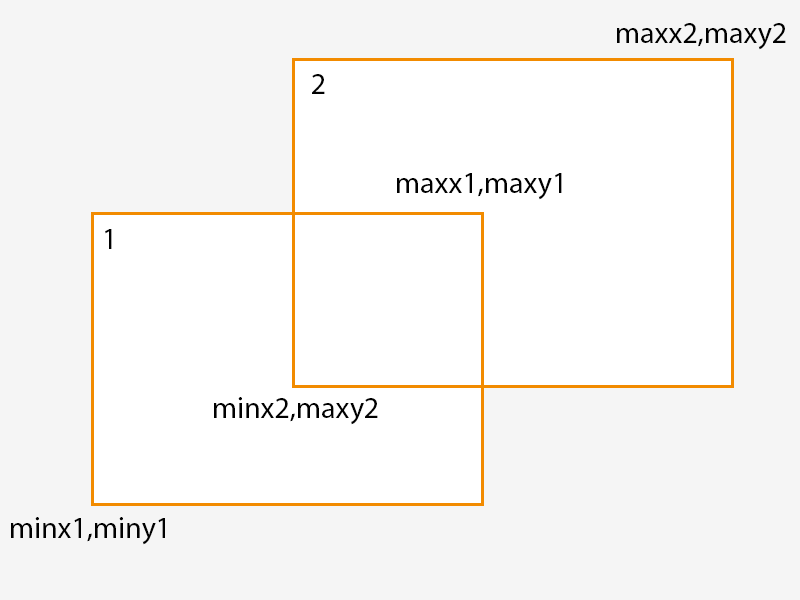
在此图中,我们有两个由一对点定义的 AABB,以下表达式的结果可以确定它们是否相交:
maxx1 > minx2 && minx1 < maxx2 && maxy1 > miny1 && miny1 < maxy2关于该表达式需要注意的重要一点是,它由一系列 and 组成,这意味着一旦其中一个条件失败,评估就会停止。
我很幸运在体素引擎中工作,因为我的游戏世界中的对象自然是轴对齐的:体素本质上是 3d 像素或微小的立方体。 但是,如果你的对象没有自然对齐或由盒子以外的形状组成怎么办? 这就是 AABB 边界部分的用武之地,因为你需要创建一个包含复杂形状的边界框,如下图所示:

显然,测试交叉点的 AABB 不会导致像素完美的碰撞检测,但请记住使用 AABB 的主要目标是在过程的广泛范围内。 快速且廉价地确定上图中的两个 AABB 不相交后,我们可以节省尝试找出两个复杂形状是否相交的计算费用。
2、AABB 树
使用上述方法,你可以看到我们如何快速、轻松地测试世界空间中两个对象之间的碰撞,但是如果有 100 个对象怎么办? 还是1000? 无论单个测试的效率如何,将 1000 个 AABB 与自身进行比较将是一项昂贵的操作并且非常浪费。
这就是 AABB 树的用武之地。它允许我们组织和索引我们的 AABB,以最大限度地减少 AABB 交叉测试的数量,而这些测试需要通过使用更多 AABB 来分割世界来进行。
可能你之前没有遇到过它们,树是非常有用的分层数据结构,并且基本概念有很多变体。如果你对这些事情感兴趣,那么一本关于该主题的优秀且相当正式的书是《算法导论》,然后再继续从这篇维基百科文章中获得结构和术语的基本知识是值得的。
就此处介绍的 AABB 树而言,根、枝和叶具有一些非常具体的属性:
- 分支—我们的分支总是有两个子分支(称为左分支和右分支),并被分配一个足够大的 AABB 来包含它的所有后代。
- 叶子 – 我们的叶子与游戏世界对象相关联,并通过它拥有 AABB。 叶子的 AABB 必须完全适合它的父母 AABB,并且由于我们的分支的定义方式,这意味着它适合每个祖先 AABB。
- 根—我们的根可能是一根树枝,也可能是一片叶子
说明其工作原理的最佳方式是通过一个实际示例。
3、构建 AABB 树
想象一下我们有一个空的世界,所以此时我们的树是空的,我们正在向其中添加第一个对象。 由于我们的树当前是空的,我们创建一个与新对象相对应的叶节点,并共享其 AABB 并将该叶节点指定为根:

现在我们向世界添加第二个对象,它与我们的第一个节点不相交,并且我们的树发生了一些有趣的事情:
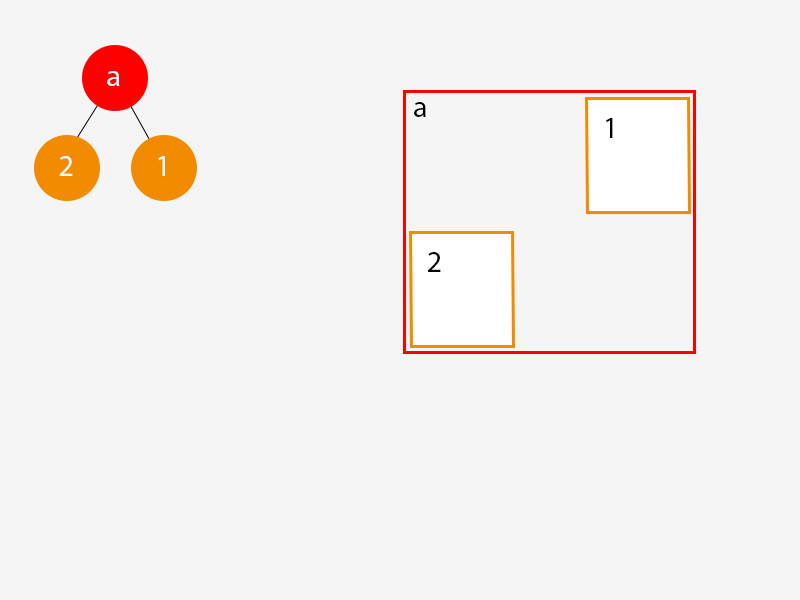
当我们将第二个对象添加到游戏世界时,发生了很多事情:
- 我们为树创建了一个分支节点,并为其分配了一个足以容纳对象 (1) 和对象 (2) 的 AABB。
- 我们为对象 (2) 创建了一个新的叶节点并将其附加到我们的新分支节点。
- 我们将对象 (1) 的原始叶节点附加到新的分支节点。
- 我们将新的分支节点作为树的根。
好的。 让我们向游戏世界添加另一个对象,这次我们将让它与现有对象相交:
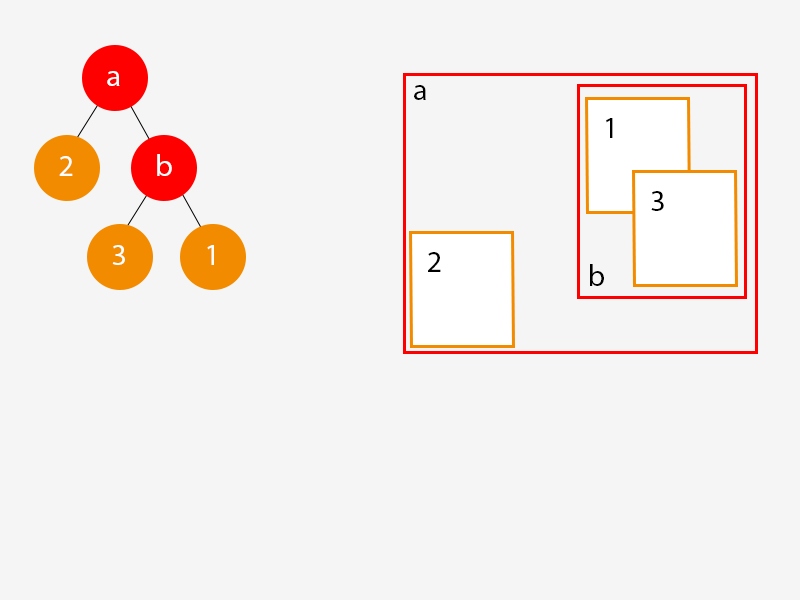
当我们添加这个对象时,我们的树又发生了一些有趣的事情:
- 我们创建了一个新的分支节点 (b),并为其分配了一个包含对象 (1) 和 (3) 的 AABB。
- 我们为对象(3)创建了一个新的叶节点并将其分配给分支(b)。
- 我们将叶节点 (1) 移动为分支节点 (b) 的子节点,并附加这个新的分支节点 (b) 分支节点 (a)。
- 这很微妙但很重要:我们调整了分配给分支节点 (a) 的 AABB,以便它考虑新的叶节点。 如果我们没有这样做,分配给分支节点 a 的 AABB 将不再大到足以容纳其后代的 AABB。
本质上,每次我们添加新的游戏世界对象时,我们都会操纵树,以便我之前描述的分支和根节点的规则仍然适用。 在这种情况下,我们可以描述将新游戏世界对象添加到树中的通用过程:
- 为对象创建一个叶节点,并根据其关联对象为其分配 AABB。
- 找到树中最好的现有节点(叶子或分支),使新叶子成为其兄弟节点。
- 为找到的节点和新的叶子创建一个新的分支节点,并为其分配一个包含两个节点的 AABB(实质上组合了两个找到的节点和新叶子的 AABB)。
- 将新叶子附加到新分支节点。
- 从树中删除现有节点并将其附加到新分支节点。
- 将新分支节点附加为现有节点的前一个父节点的子节点。
- 回到树上调整我们所有祖先的 AABB,以确保它们仍然包含所有后代的 AABB。
上面的第 2 步确实提出了一个问题:如何找到树中最好的叶子,使新叶子成为其兄弟节点? 本质上,这涉及到沿着树下降并评估附着到你移动经过的每个分支的左侧或右侧的可能成本。 你做出的决定越好,树就越平衡,后续查询的成本就越低。
这里使用的一个常见的启发式方法是为左右节点的表面积分配一个成本,该表面积已针对添加新叶子的 AABB 进行了调整,并沿着最便宜节点的方向下降,直到发现自己位于叶子上。
4、查询AABB树
这就是我们所有的辛勤工作得到回报的地方—它非常简单而且非常快。 如果我们想要找到给定 AABB 对象的所有可能的碰撞,我们需要做的就是从树的根部开始:
- 检查当前节点是否与测试对象 AABB 相交。
- 如果是,并且它是叶节点,那么这是一次冲突,因此将其添加到冲突列表中。
- 如果是并且是分支节点,则向左和向右下降并递归地重复此过程。
在上面的末尾,你的列表将包含测试对象的所有可能的碰撞,并且我们将最大限度地减少必须执行的 AABB 交叉检查的数量,因为我们不会沿着任何路径下降(因此所有后续子级) 无法与测试 AABB 树相交。
在实现中,最好不要实际使用递归方法,因为这在大型树上可能会变得昂贵(并且可能会失败)。 相反,只需维护要进一步探索的节点堆栈/列表,如下所示:
- 将根节点推入堆栈(在 C++ 中我使用 std::stack)
- 当堆栈不为空时:
- 从堆栈中弹出
- 检查节点是否与测试 AABB 对象相交
- 如果是这样,那么:
- 如果它是叶节点,则这是碰撞匹配。 将叶节点(或其引用的对象)添加到冲突列表中。
- 如果它是分支节点,则将子节点(左节点和右节点)推入堆栈。
了解如何非递归地迭代树非常有用。
5、更新 AABB 树
在大多数(但不是全部)涉及碰撞检测的场景中,世界上至少有一些物体正在移动。 当对象移动时,确实需要更新树,这是通过删除与世界对象相对应的叶子并重新插入它来完成的。
这可能是一项昂贵的操作,如果你使用速度向量表达世界对象的运动并使用它来“增肥”插入到树中的 AABB 树,则可以最大限度地减少执行此操作的次数。 例如,采用下图中的对象,它的 (x,y) 速度为 (1,0),并且其边界 AABB 相应地变厚:

AABB 树的增肥程度是更新成本、可预测性和大范围精度之间的权衡,您可能需要进行试验才能获得最佳性能。
最后,随着树的更新,它们可能会变得不平衡,因为某些查询不适当地需要遍历比其他节点更多的节点。 解决此问题的一种技术是使用基于每个节点的高度(距底部的深度)的旋转来重新平衡树。 另一种方法是根据子节点如何均匀划分父节点 AABB 来平衡树。 这稍微超出了初学者指南的范围,而且我还没有在示例代码中亲自实现它——但是我可能会在某个时候返回它。
6、示例代码
最后是这篇博客文章附带的示例代码,你可以在我的游戏引擎中找到它。 它与引擎本身相当分离,你应该能够在自己的代码中使用它,而不会出现太多问题。 关键文件是:
- AABB.h – 定义用于表示和操作 AABB 的结构
- AABBTree.h – 定义树类 AABBTree 和 AABBNode 结构入口点的头文件
- AABBTree.cpp – 实现
- IAABB.h – 定义添加到树中的对象必须实现的接口
要使用树,你需要将这四个文件添加到你的项目中并构造 AABBTree 类的实例 - 它的构造函数非常简单,并且需要一个初始大小(要预先保留的树节点的数量)。 你想要添加到树中的任何对象都需要实现 IAABB 接口,该接口只需要在需要时返回 AABB 结构。 你可以分别使用 insertObject、 updateObject 和 removeObject 方法添加、更新和删除这些对象,并且可以使用 queryOverlaps 方法查询冲突。
7、有用的链接
在研究 AABB 树时,我发现了一些有用的链接,如下所示。
特别是,我发现最后两个链接中的代码非常适合阅读,并且能够在此基础上构建我自己的代码,特别是节点分配。
原文链接:Introductory Guide to AABB Tree Collision Detection
BimAnt翻译整理,转载请标明出处





