NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模
你是否曾经对张量维度的工作原理感到困惑,尤其是当你需要在高维度上应用 sum() 等操作时? 你在这篇文章中学到的技术不仅适用于张量维度,也适用于 Numpy ndarray 维度,因为多维数组/张量的逻辑是相同的。
本文将以一种直观的方式来可视化 sum() 运算在张量维度上的工作原理,并使用 Pytorch 检查代码中张量和的示例。
1、张量的形状(维度)
首先,张量只是多维数组的另一个名称。 当数学家定义了术语:标量(0D)、向量(1D)、矩阵(2D)时,我们需要一个高维的通用术语和概念。
这是一个张量,我们可以通过计算每一层括号的数量来找到张量的形状。 请注意,最外面的括号将被忽略,因为它只是用来包裹整个对象。


所以这里我们在最外层有 2 个元素 (dim: 0),在第二层有 3 个元素 (dim: 1),在最内层有 3 个元素 (dim: 2)。 因此,张量的形状为(2,3,3)。
2、Dim 0 求和
接下来,我们将对维度 0 求和,我们只需要遵循 3 个简单的步骤:
- 识别维度中的元素。
- 重叠这些元素。
- 用X光眼将出现在同一位置的数字相加。
就是这样! 分步说明如下:
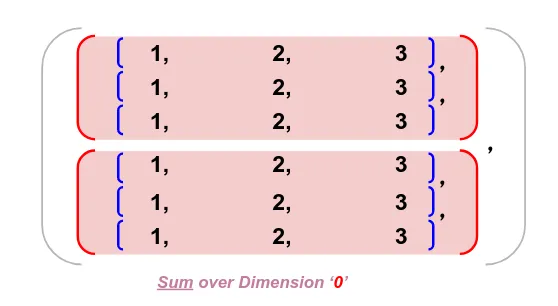



注意:当你对张量中的dim i 求和时,会将dim i 减少到 1,因为将该维度中的每个数字相加,并将多个数字减少为一个总和。 你会看到这种情况发生在各个维度。
现在,我们已经了解了它在维度 0 上的工作原理,让我们在维度 1 上挑战相同的步骤。
3、Dim 1 求和
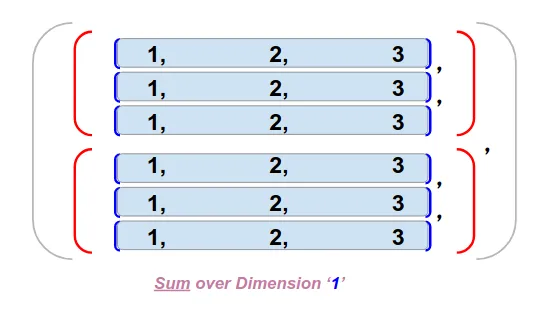

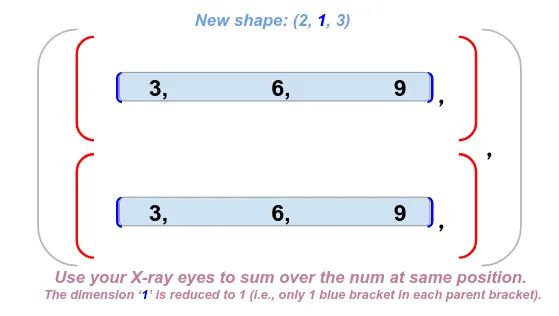
注意:在对dim 1 求和之后,dim 1 上也会发生相同的维度缩减,并且求和后的新形状已缩减为 (2,1,3)。
我们只需要将相同的步骤进行到最后一个维度即可。
4、Dim 2 求和
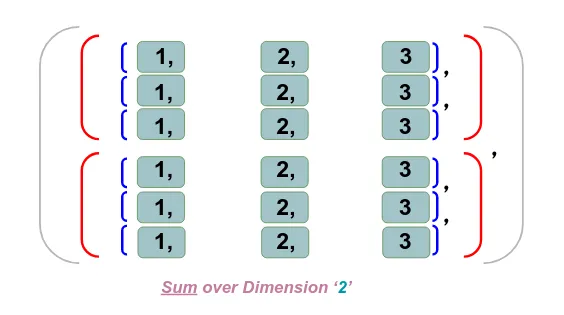
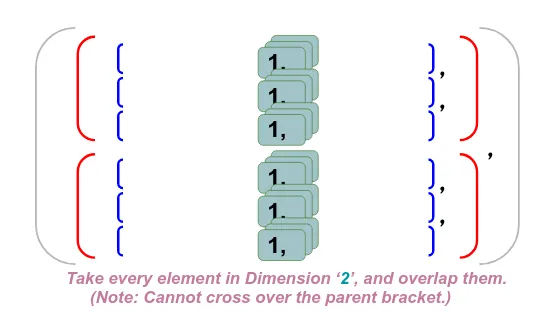
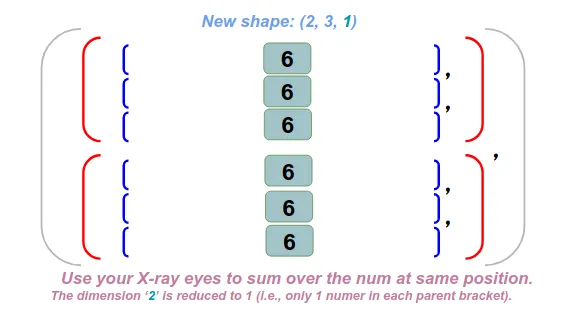
注意:在我们对 dim 2 求和之后,同样的降维也发生在 dim 2 上,并且求和后的新形状已减少到 (2,3,1)。
现在我们已经了解了张量 sum() 运算的工作原理,让我们用代码来实现。
5、使用Pytorch执行张量求和
下面的 Jupyter Notebook 展示了我们如何执行张量 sum() 并检查我们对其维度的理解。
import torch
x = torch.FloatTensor([
[2.,1.],
[2.,1.],
[2.,1.]
])
torch.sum(x, dim=0, keepdim=True)
x = torch.FloatTensor([
[2.,1.],
[2.,1.],
[2.,1.]
])
torch.sum(x, dim=1, keepdim=True)
x = torch.FloatTensor([
[2.,1.],
[2.,1.],
[2.,1.]
])
torch.sum(x, dim=-1, keepdim=True)
x = torch.FloatTensor([[
[1.,2.,3.],
[1.,2.,3.],
[1.,2.,3.]
],[
[1.,2.,3.],
[1.,2.,3.],
[1.,2.,3.]
],
])
torch.sum(x, dim=0, keepdim=True)
x = torch.FloatTensor([[
[1.,2.,3.],
[1.,2.,3.],
[1.,2.,3.]
],[
[1.,2.,3.],
[1.,2.,3.],
[1.,2.,3.]
],
])
torch.sum(x, dim=1, keepdim=True)
x = torch.FloatTensor([[
[1.,2.,3.],
[1.,2.,3.],
[1.,2.,3.]
],[
[1.,2.,3.],
[1.,2.,3.],
[1.,2.,3.]
],
])
torch.sum(x, dim=2, keepdim=True)
x = torch.FloatTensor([[
[1.,2.,3.],
[1.,2.,3.],
[1.,2.,3.]
],[
[1.,2.,3.],
[1.,2.,3.],
[1.,2.,3.]
],
])
torch.sum(x, dim=-1, keepdim=True)注意:在函数中,你需要指定 keepdim=True 以保留其原始尺寸,如我们在第一个直观部分中展示的那样。 否则,减少到 1 的维度将被简单地删除。
7、结束语
这是我在努力理解高维张量上的运算符(例如 sigmoid、max、sum 等)时自学的最直观的可视化,我希望本文能够增强你的张量直觉,让你快速识别张量维度!
原文链接:An Intuitive Understanding on Tensor Dimension with Pytorch — Using torch.sum() as Example
BimAnt翻译整理,转载请标明出处





