NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模
最近,拥有数十亿个参数的大型神经网络引起了大量关注,这是理所当然的。通过将大量参数与transformer和扩散等强大的架构相结合,神经网络能够完成惊人的壮举。
但是,即使是小型网络也可能出奇地有效 - 尤其是当它们是专门为特定用例设计的。作为我之前所做的一些工作的一部分,我正在训练小型(<1000 个参数)网络来生成序列到序列的映射并执行其他简单的逻辑任务。我希望模型尽可能小而简单,目标是构建其内部状态的小型交互式可视化。
在非常简单的问题上取得成功后,我尝试训练神经网络执行二进制加法。网络将接收两个 8 位无符号整数的位作为输入(将位转换为浮点数,二进制 0 为 -1,二进制 1 为 +1),并有望产生正确添加的输出,包括处理溢出包装。
二进制训练示例:
01001011 + 11010110 -> 00100001作为 NN 训练的输入/输出向量:
input: [-1, 1, -1, -1, 1, -1, 1, 1, 1, 1, -1, 1, -1, 1, 1, -1]
output: [-1, -1, 1, -1, -1, -1, -1, 1]我希望/想象网络内部能够学习到类似于二进制加法器电路的东西:
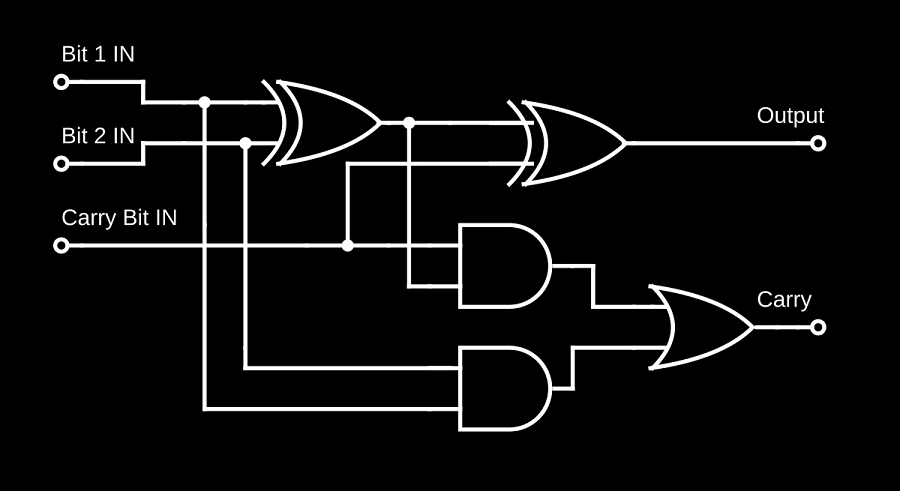
我期望它能够识别输入和输出中不同位之间的关系,根据需要路由它们,并使用神经元作为逻辑门 - 我过去在测试其他问题时看到过这种情况。
1、训练网络
首先,我创建了一个具有相当丰富架构的网络,该网络有 5 层和几千个参数。但是,我不确定这是否足够。上面的二进制加法器逻辑电路图仅处理单个位;将 8 位加到 8 位需要大量的门,并且网络必须对所有门进行建模。
此外,我不确定网络如何处理长链进位。例如,当添加 11111111 + 00000001 时,它会回绕并产生输出 00000000。为了实现这一点,最低有效位的进位需要通过加法器一直传播到最高有效位。我认为网络很可能需要至少 8 层才能实现这种行为。
尽管我不确定它是否能够学到任何东西,但我还是开始训练模型。
我通过生成随机的 8 位无符号整数并将它们加在一起并进行包装来创建训练数据。除了在网络训练期间计算的损失之外,我还添加了代码以在训练期间定期验证网络在所有 32,385 种可能的输入组合上的准确性,以了解它的整体表现。
在对学习率和批量大小等超参数进行一些调整后,我惊讶地发现模型学习得非常好!我能够让它达到几乎每次训练运行都能收敛到完美或近乎完美的解决方案的程度。
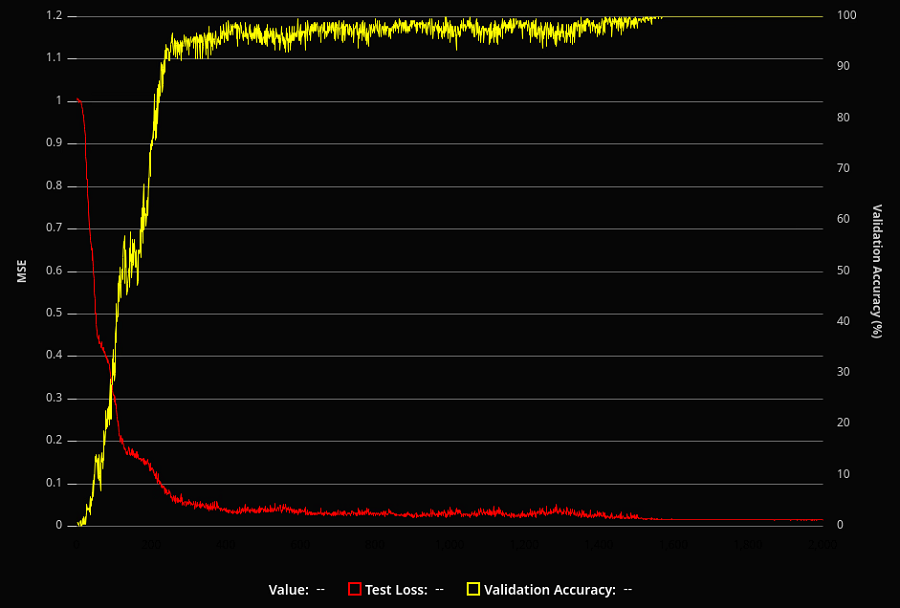
我想知道网络内部是如何生成解决方案的。我训练的网络对于手头的任务来说参数化程度相当高;很难通过数以万计的权重和偏差来了解它们在做什么。因此,我开始精简网络 - 删除层并减少每层的神经元数量。
令我惊讶的是,它一直在工作!在某种程度上,完美的解决方案变得不那么常见,因为网络变得依赖于其起始参数的运气,但我能够让它在只有 3 层、神经元数量分别为 12、10 和 8 的情况下学习完美的解决方案:
Layer (type) Input Shape Output shape Param #
===========================================================
input1 (InputLayer) [[null,16]] [null,16] 0
___________________________________________________________
dense_Dense1 (Dense) [[null,16]] [null,12] 204
___________________________________________________________
dense_Dense2 (Dense) [[null,12]] [null,10] 130
___________________________________________________________
dense_Dense3 (Dense) [[null,10]] [null,8] 88
===========================================================那总共只有 422 个参数!我没想到网络能够用这么少的参数来学习像二进制加法这样的复杂函数。
说实话,这似乎好得令人难以置信,我想确保我在训练网络或验证其输出的方式上没有犯任何错误。对我的示例生成代码和训练管道的审查并没有发现任何不对劲的地方,所以下一步是在成功训练运行后实际查看参数。
2、独特的激活函数
此时要注意的一件重要事情是模型中不同层使用的激活函数。我之前在这个领域的部分工作包括设计和实现一种用于神经网络的新激活函数,目标是尽可能高效地执行二进制逻辑。除其他外,它能够在单个神经元中建模任何 2 输入布尔函数 - 这意味着它解决了 XOR 问题。
你可以在我的其他帖子中阅读有关它的更多详细信息,但它看起来像这样:

它看起来有点像一个平坦正弦波的单个周期,并且它有几个可控制的参数来配置它的平坦程度以及它如何处理超出范围的输入。
对于我训练的二进制加法模型,它们都在第一层使用了这个激活函数(我将其命名为 Ameo),并在所有其他层中使用了 tanh。
3、剖析模型
虽然参数数量现在相当可控,但我无法仅通过查看它们来判断发生了什么。但是,我确实注意到有很多参数非常接近“整数”值,例如 0、1、0.5、-0.25 等。
由于我之前建模的许多逻辑门都是用这些参数生成的,所以我认为这可能是一件好事,可以专注于在噪声中找到信号。
我添加了一些舍入和钳位,这些应用于所有比某个阈值更接近这些整数值的网络参数。我在整个训练过程中定期应用它,让优化器有时间适应其间的变化。经过几次重复并等待网络再次收敛到完美解决方案后,一些清晰的模式开始出现:
layer 0 weights:
[[0 , 0 , 0.1942478 , 0.3666477, -0.0273195, 1 , 0.4076445 , 0.25 , 0.125 , -0.0775111, 0 , 0.0610434],
[0 , 0 , 0.3904364 , 0.7304437, -0.0552268, -0.0209046, 0.8210054 , 0.5 , 0.25 , -0.1582894, -0.0270081, 0.125 ],
[0 , 0 , 0.7264696 , 1.4563066, -0.1063093, -0.2293 , 1.6488117 , 1 , 0.4655252, -0.3091895, -0.051915 , 0.25 ],
[0.0195805 , -0.1917275, 0.0501585 , 0.0484147, -0.25 , 0.1403822 , -0.0459261, 1.0557909, -1 , -0.5 , -0.125 , 0.5 ],
[-0.1013674, -0.125 , 0 , 0 , -0.4704586, 0 , 0 , 0 , 0 , -1 , -0.25 , -1 ],
[-0.25 , -0.25 , 0 , 0 , -1 , 0 , 0 , 0 , 0 , 0.2798074 , -0.5 , 0 ],
[-0.5 , -0.5226266, 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0.5 , -1 , 0 ],
[1 , -0.9827325, 0 , 0 , 0 , 0 , 0 , 0 , 0 , -1 , 0 , 0 ],
[0 , 0 , 0.1848682 , 0.3591821, -0.026541 , -1.0401837, 0.4050815 , 0.25 , 0.125 , -0.0777296, 0 , 0.0616584],
[0 , 0 , 0.3899804 , 0.7313382, -0.0548765, -0.021433 , 0.8209481 , 0.5 , 0.25 , -0.156925 , -0.0267142, 0.125 ],
[0 , 0 , 0.7257989 , 1.4584024, -0.1054092, -0.2270812, 1.6465081 , 1 , 0.4654536, -0.3099159, -0.0511372, 0.25 ],
[-0.125 , 0.069297 , -0.0477796, 0.0764982, -0.2324274, -0.1522287, -0.0539475, -1 , 1 , -0.5 , -0.125 , 0.5 ],
[-0.1006763, -0.125 , 0 , 0 , -0.4704363, 0 , 0 , 0 , 0 , -1 , -0.25 , 1 ],
[-0.25 , -0.25 , 0 , 0 , -1 , 0 , 0 , 0 , 0 , 0.2754751 , -0.5 , 0 ],
[-0.5 , -0.520548 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0.5 , 1 , 0 ],
[-1 , -1 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , -1 , 0 , 0 ]]
layer 0 biases:
[0 , 0 , -0.1824367,-0.3596431, 0.0269886 , 1.0454538 , -0.4033574, -0.25 , -0.125 , 0.0803178 , 0 , -0.0613749]以上是经过限制和舍入后为网络第一层生成的最终权重。每列代表单个神经元的参数,这意味着从上到下的前 8 个权重应用于第一个输入数字的位,而接下来的 8 个权重应用于第二个输入数字的位。
所有这些神经元最终都处于非常相似的状态。有一种模式是,当它们沿着线向下移动时,权重会加倍,并在两个输入的相应位之间匹配权重。选择偏差以匹配最小的权重。不同的神经元具有不同的乘数基数和不同的起始数字偏移量。
4、网络学到的巧妙解决方案
经过一段时间的思考,我最终开始明白它的解决方案是如何工作的。
数模转换器 (DAC) 是一种电子电路,它将数字信号分成多个输入位,并将其转换为单个模拟输出信号。
DAC 用于音频播放等应用中,其中声音文件由存储在内存中的数字表示。 DAC 接收这些二进制值并将其转换为模拟信号,用于为扬声器供电、确定其位置并振动空气以产生声音。例如,任天堂 Game Boy 的两个输出音频通道各有一个 4 位 DAC。
以下是 DAC 的示例电路图:
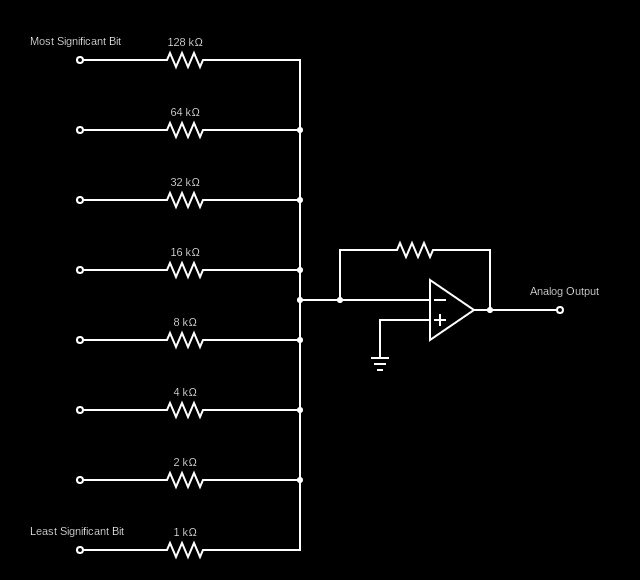
如果你查看连接到二进制输入的每个位的电阻器的电阻,会发现它们从一个输入到另一个输入从最低有效位到最高有效位加倍。这与网络学会对输入层权重的操作非常相似。主要区别在于权重在两个 8 位输入之间重复。
这允许网络在单个层/神经元内对输入求和以及将总和转换为模拟,并且在任何激活函数发挥作用之前完成所有操作。
不过,这只是难题的一部分。一旦数字输入转换为模拟并相加,它们就会立即通过神经元的激活函数。为了帮助追踪接下来发生的事情,我绘制了第一层中一些神经元在输入增加时的激活后输出:
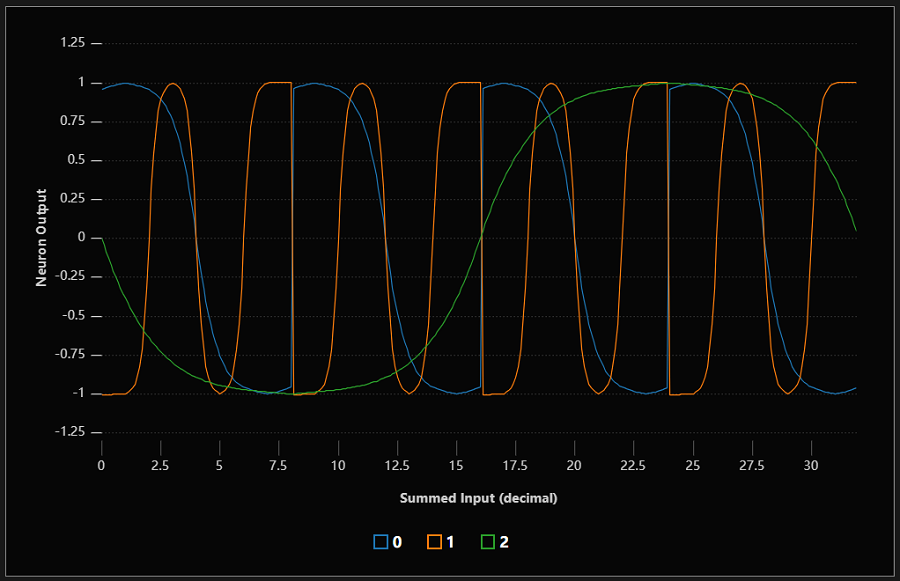
神经元似乎在产生正弦波状的输出,这些输出随着二进制输入总和的增加而平稳变化。不同的神经元有不同的周期;上图所示的神经元周期分别为 8、4 和 32。其他神经元的周期不同或偏移一定距离。
这种模式非常引人注目:它们直接映射到二进制计数时不同二进制数字在 0 和 1 之间切换的周期。最低有效数字在 0 和 1 之间切换的周期为 1,第二个数字在 2 之间切换的周期为 2,依此类推,4、8、16、32 等。这意味着,对于至少一些输出位,网络已经学会在单个神经元中计算所需的一切。
查看后面两层神经元的权重可以证实情况确实如此。后面的层主要关注绕过第一层的输出并将它们组合起来。这些层提供的另一个好处是“饱和”信号并使其更像方波 - 使它们更接近所有值的目标值 -1 和 1。这与数字信号处理中用于音频合成的属性完全相同,其中 tanh 用于为吉他踏板等声音添加失真。
在尝试这个设置时,我尝试用 sin(x) 替换第一层的激活函数重新训练网络,最终它的工作方式几乎相同。有趣的是,在这种情况下学习到的权重是 π 的分数,而不是 1。
对于其他输出数字,网络学会了一些非常巧妙的事情来生成它所需的输出信号。例如,它以这样一种方式组合了第一层的输出,即它能够通过将来自其他具有不同周期的神经元的信号加在一起来产生第一层神经元中不存在的信号的移位版本。它的效果非常好,对于网络的目的来说已经足够准确了。
网络学习到的基于正弦的函数版本(蓝色)最终大致相当于函数 sin(1/2x + pi)(橙色):
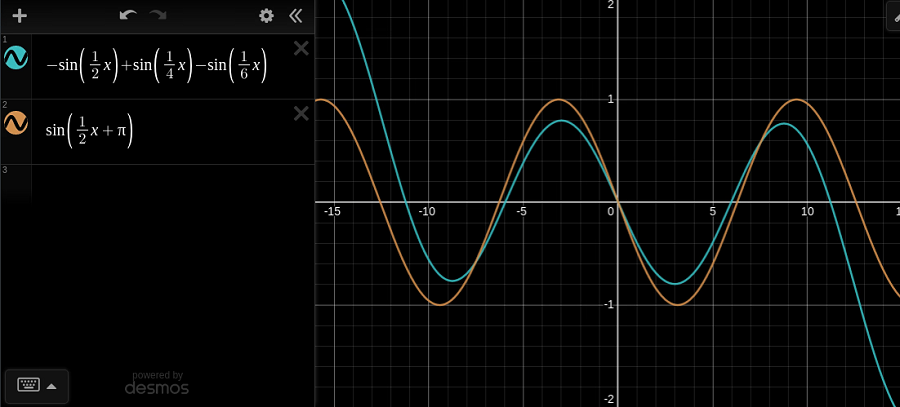
我不知道这是否只是另一个随机的数学巧合或某个无限级数的一部分,但无论如何它非常巧妙。
5、总结
因此,总的来说,网络通过以下方式完成二进制加法:
- 使用使用输入层权重实现的数模转换器版本将二进制输入转换为“模拟”
- 使用 Ameo 激活函数将内部模拟信号映射到周期性正弦波状信号(即使该激活函数不是周期性的)
- 使正弦波状信号饱和以使其更像方波,以便输出尽可能接近所有输出的预期值 -1 和 1
正如我之前提到的,我曾想象网络学习一些奇特的逻辑门组合来以数字方式执行整个加法过程,类似于二进制加法器的操作方式。这个技巧是神经网络找到意想不到的解决问题方法的另一个例子。
6、结束语
在这次调查之后,我想到了一个前提,即通过使用更高效或定制设计的架构,今天拥有数十亿个参数的庞大前沿模型可能能够使用数量级更少的网络资源来构建。
这无疑是一个令人兴奋的前景,但我的兴奋感有些减弱,因为我立刻想起了痛苦的教训。如果你还没有读过,你应该现在就读一读(它很短);它确实影响了我对计算和编程的看法。
即使这个特定的解决方案只是我的网络架构或正在建模的系统的侥幸,它也让我对梯度下降和类似优化算法的强大和多功能性更加印象深刻。这些非常特殊的模式能够如此一致地从纯粹的随机性中产生,这一事实对我来说真的很神奇。
原文链接:Reverse Engineering a Neural Network's Clever Solution to Binary Addition
BimAnt翻译整理,转载请标明出处





