NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模
包围体(Bounding Volume)在视频游戏中有很多应用。 在物理引擎中,包围体用于游戏对象之间的宽相相交测试,希望它们的(更简单的)测试减少花费在更复杂和更准确的相交测试上的周期数。 在图形引擎中,边界体积根据相机的视锥体进行测试 - 相机视图之外的对象,随后被剔除并且不被绘制,从而节省宝贵的时间并保持可播放的帧速率。
在使用的各种包围体中,我们将重点关注有向包围盒,简称 OBB,即Oriented Bounding Box。
与轴对齐边界框 (AABB) 不同,OBB 的面不必与三个坐标平面中的任何一个平行。
给定一组顶点(例如,网格),很容易生成边界 AABB。 然而,我们想问的问题是,给定相同的顶点集,我们如何生成理想的OBB?
我们将使用统计学和数值线性代数的概念来解决这个问题。
1、主成分分析
当收集线性系统的数据时(我们的 OBB 边缘是直的),存在三种可能的混淆来源:
- 噪音
- 旋转
- 冗余
噪声是由于我们的测量不准确而产生的,而旋转则是由于不知道我们正在研究的系统中真正的基础变量而产生的,例如,我们很可能正在测量真实变量的(希望是线性的)组合。
最后,冗余源于不知道我们正在测量的变量是否独立,并且我们可能正在测量同一组变量的一个或多个(再次希望是线性的)组合。
主成分分析(PCA)是一种使用正交变换(旋转)的技术,将一组可能相关变量的观测值(我们的顶点云)转换为一组称为主成分的线性不相关变量的值。 在此过程中,它使用数据集完成了三件事:
- 隔离噪音
- 消除旋转的影响
- 分离出多余的自由度
在统计学中,两个变量之间的协方差衡量两个变量之间线性关系的程度。 小值表示变量是独立的(无相关性)。
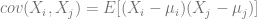
请注意,变量与其自身的协方差只是该随机变量的方差。
然后得出协方差矩阵,该矩阵的 (i ,j) 位置元素是随机变量向量的第 i 个和第 j 个元素之间的协方差。 本质上,协方差矩阵将方差的概念推广到多个维度。
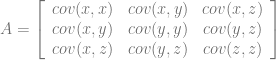
矩阵的对角线元素是变量的方差。 大的对角线元素对应于强信号。非对角线元素是变量之间的协方差。 大的非对角线元素对应于我们数据中的扭曲。
为了最大限度地减少失真,如果我们重新定义变量(作为彼此的线性组合),那么协方差矩阵将会改变。 特别是,我们想要更改协方差矩阵,使得非对角线元素接近于零,因此我们想要对角化协方差矩阵。
请注意,协方差矩阵是实值且对称的,这意味着当我们进行对角化时,我们保证在相似变换(基矩阵的变化)中具有三个特征向量。
重点是——协方差矩阵的特征向量构成了 OBB 的方向。 大特征值对应大方差,因此我们应该沿着与最大特征值对应的特征向量对齐 OBB。
2、示例:计算2D点集的有向包围盒
下面是一个2D的例子。假设我们要为以下十个点的数据集生成 OBB:
(3.7, 1.7), (4.1, 3.8), (4.7, 2.9), (5.2, 2.8), (6.0, 4.0), (6.3, 3.6), (9.7, 6.3), (10.0, 4.9), (11.0, 3.6), (12.5, 6.4)
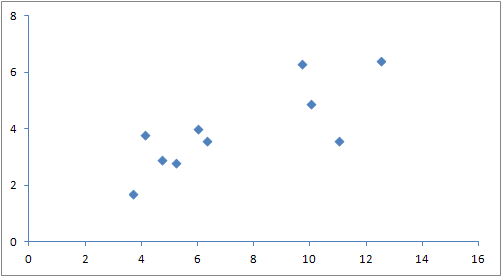
通过数学计算,我们计算方差和协方差,从而得出以下协方差矩阵:
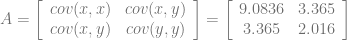
这会导致以下相似变换:

然后我们使用 OBB 轴的特征向量:
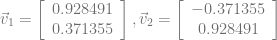
投影到这些向量上使我们能够确定 OBB 的中心和半范围长度,从而得到以下图像:
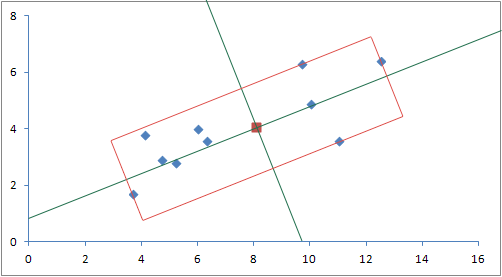
上面的 OBB 大约以 (8.10, 4.05) 为中心,半范围为 4.96 和 1.49 单位,对应于上面的两个轴向量。 OBB 轴的跨度标记为绿色。
译者注:上面的投影包含几个步骤:
1、将数据点变换到以特征向量为基的新坐标系下
2、计算变换后的数据点在各轴上的最小和最大值,求得中心点坐标和各角点坐标
3、将中心坐标和角点坐标变换回原坐标系
3、计算凸包的有向包围盒
人们可能会注意到,在上述计算中,所有顶点都在确定协方差矩阵中发挥着作用,而我们真正想做的只是计算包围体。 也就是说,网格内的顶点仍然在协方差矩阵中发挥作用,从而在最终的特征向量中发挥作用,而实际上它们不应该发挥作用,因为它们被其他顶点包含。
例如,假设我们有一个非常密集的点云,集中在网格内。 即使这些点位于网格内部并且已经被任何包围体封装,它的密度也会扭曲协方差。
我们可以通过计算构成数据集凸包的顶点的协方差矩阵来修改上述算法。 从数学上讲,集合的凸包是包含所有集合元素的最小凸集。 直观上,凸包可以看作是围绕点拉伸橡皮筋时形成的形状。
唉,实际确定集合的凸包是计算几何的基本问题之一,超出了本文的范围。
在凸包上重复上述算法会得到与之前生成的 OBB 没有太大不同的 OBB。
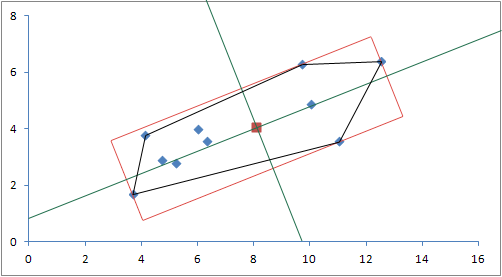
构成凸包的点集是:
{(3.7, 1.7), (4.1, 3.8), (9.7, 6.3), (11.0, 3.6), (12.5, 6.4)}。我们的协方差矩阵和随后的对角化给我们:
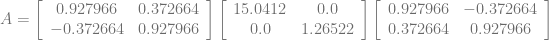
这反过来会导致 OBB 的差异超过 3 位有效数字的准确性。 就总面积而言,讽刺的是,凸包生成的 OBB 比整组生成的 OBB 大 0.000395 平方单位。
就我个人而言,当需要注意的其他事情的列表还在继续时,我认为这种微小的体积节省(如果有的话)不值得额外的计算工作(更不用说生成凸包所需的工作) 。 :)
原文链接:OBB generation via Principal Component Analysis
BimAnt翻译整理,转载请标明出处





