NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模
策略梯度方法 (PG:Policy Gradient) 是强化学习 (RL:Reinforcement Learning) 中常用的算法。
1、从库里的本能开始
PG的原理很简单:我们观察,然后行动。人类根据观察采取行动。 引用斯蒂芬·库里的一句话:
你必须依靠这样一个事实:你付出了努力来创造肌肉记忆,然后相信它会发挥作用。你如此多地练习和努力的原因是,在比赛过程中你的直觉会在一定程度上发挥作用。 如果你没有以正确的方式去做,就会感觉很奇怪。

不断的练习是运动员建立肌肉记忆的关键。 对于 PG,我们训练一个基于观察来采取行动的策略。 PG 中的训练使得高奖励的行动更有可能发生,反之亦然。
我们保留有效的,丢弃无效的。
在策略梯度方法中,库里是我们的代理人。
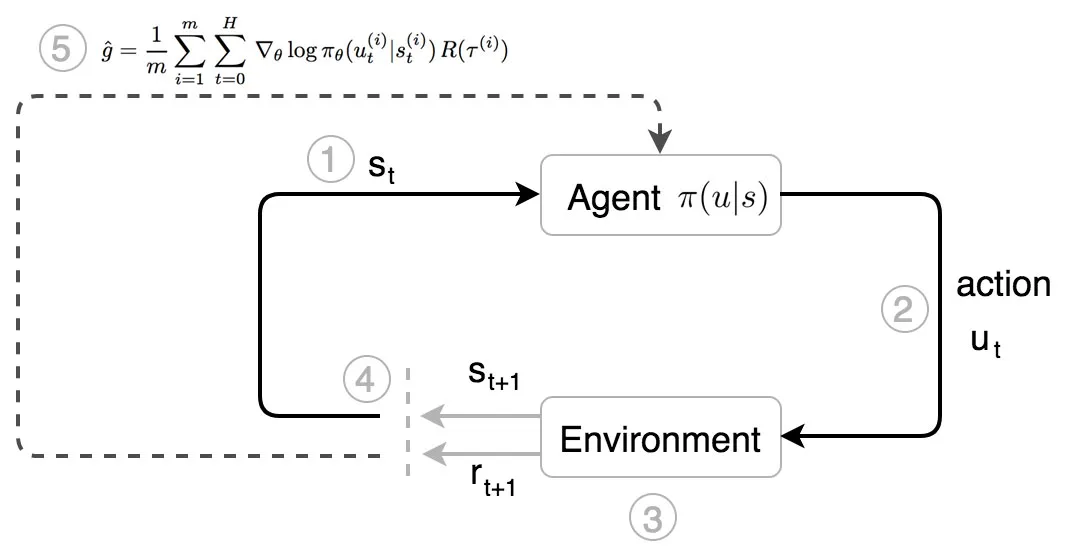
- 他观察环境的状态。
- 他根据自己对状态 s 的本能(策略 π)采取行动(u)。
- 他移动,对手做出反应。 一个新的状态形成了。
- 他根据观察到的状态采取进一步的行动。
- 经过 运动轨迹τ 后,他根据收到的总奖励 R(τ) 调整自己的本能。
库里看到了情况并立即知道该怎么做。 多年的训练完善了最大化回报的本能。 在强化学习中,本能可以在数学上描述为:

即在给定状态 s 的情况下采取动作 u 的概率。 π 是强化学习中的策略。 例如,当你看到前面有车时转弯或停车的机会有多大:

2、策略梯度的学习目标
我们如何用数学方式制定我们的目标? 期望得到的奖励等于轨迹的概率×相应奖励之和:
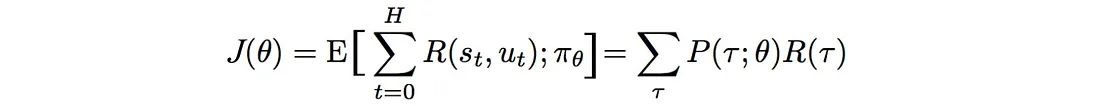
我们的目标是找到策略 θ,使其可以创建轨迹 τ :
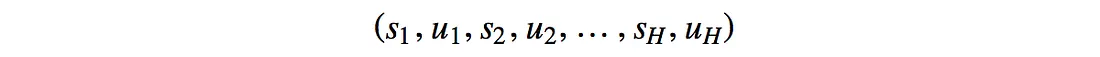
而轨迹τ能够最大化预期回报:

3、输入特征和奖励
策略梯度方法的输入(即状态s)可以是手工制作的状态特征(如机械臂关节的角度、速度等),但在某些问题领域,强化学习已经足够成熟,可以直接处理原始图像。 π 可以是一个确定性策略,它输出要采取的确切操作(如向左或向右移动操纵杆),也可以是一个随机策略,它输出它可能采取的行动的可能性。
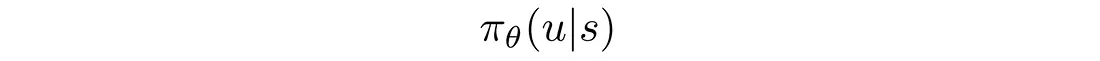
我们记录每个时间步给出的奖励 r。 在篮球比赛中,除了终止状态为0、1、2或3外,其他状态均为0。

我们再引入一个术语 H,称为地平线。 我们可以无限期地运行模拟过程(h→∞),直到达到终止状态,或者我们对 H 步设置限制。
4、优化问题
首先,让我们回顾一下深度学习和强化学习中常见且重要的技巧,函数 f(x) (R.H.S.) 的偏微分等于 f(x) 乘以 log(f(x)) 的偏微分:
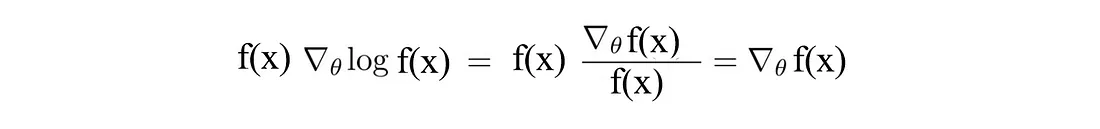
将 f(x) 替换为 π,得到:
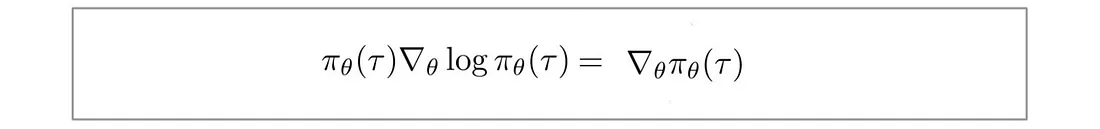
另外,对于连续空间,期望可以表示为:
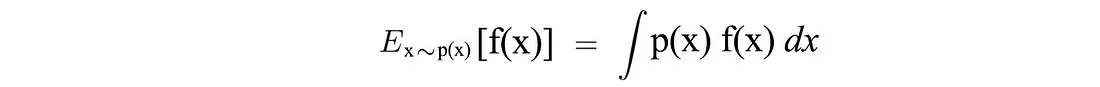
现在,让我们用数学形式形式化我们的优化问题。 我们想要建立一个策略模型,该模型能够产生最大化总回报的轨迹:
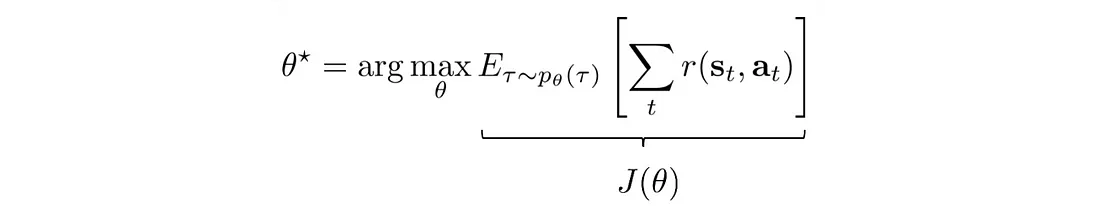
然而,要使用梯度下降来优化我们的问题,我们是否需要对奖励函数 r 求导,而该导数可能不可微分或形式化?
让我们将目标函数 J 重写为:

梯度(策略梯度)变成:
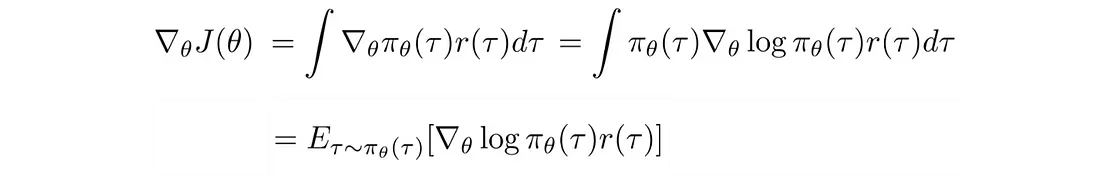
好消息! 策略梯度可以表示为期望, 这意味着我们可以使用采样来近似它。 此外,我们对 r 的值进行采样,但不对其进行微分。 这是有道理的,因为奖励并不直接取决于我们如何参数化模型,但轨迹 τ 是。 那么log π(τ) 的偏导数是多少。
π(τ) 定义为:
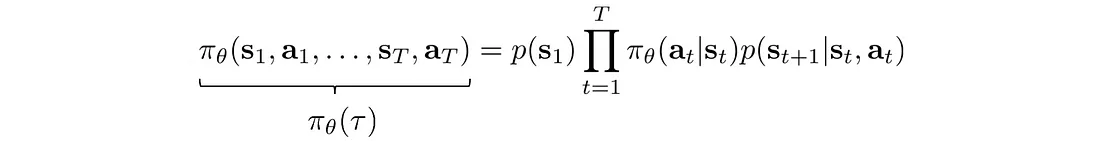
取对数:

第一项和最后一项不依赖于 θ,可以删除。

所以策略梯度:
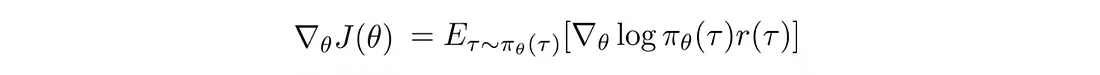
变成:
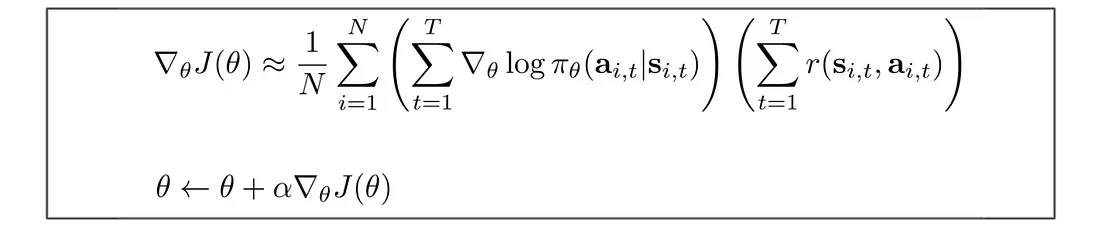
我们使用这个策略梯度来更新策略θ。
5、关于梯度更新的直觉
我们如何理解这些公式?
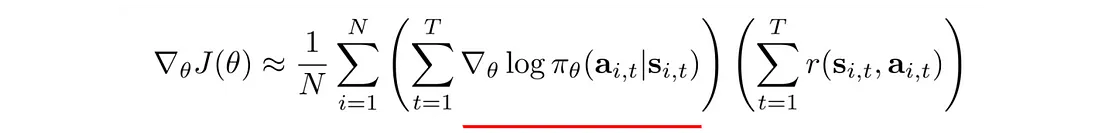
下划线项是最大对数似然。 在深度学习中,它测量观察到的数据的可能性。 在我们的背景下,它衡量当前策略下轨迹的可能性。 通过将其与奖励相乘,如果轨迹产生高额正奖励,我们希望增加策略的可能性。 相反,如果一个策略导致较高的负面回报,我们希望降低该策略的可能性。 简而言之,保留有效的,丢弃无效的。
如果爬上山意味着更高的奖励,我们将更改模型参数(策略)以增加轨迹向上移动的可能性:

策略梯度有一件重要的事情。 轨迹的概率定义为:
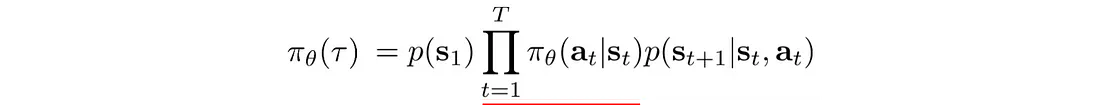
轨迹中的状态密切相关。 在深度学习中,与强相关因子的长序列相乘很容易触发梯度消失或梯度爆炸。 然而,策略梯度只是对梯度进行求和,从而打破了长序列相乘的诅咒。
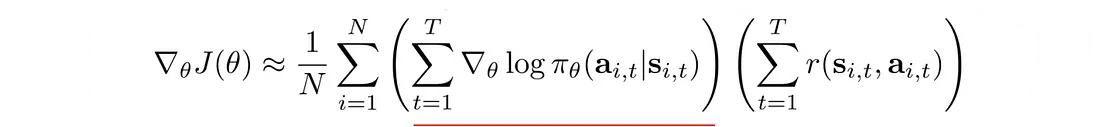
这使用了一个小技巧:
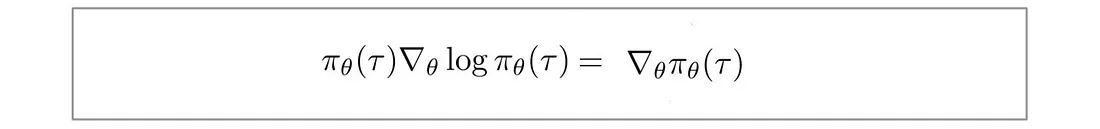
创建最大对数似然,并且对数打破了长链策略相乘的诅咒。
6、基于蒙特卡洛走子的策略梯度
下面是使用Monte Carlo rollouts来计算奖励的强化学习算法。 即播放整个情节(episode)来计算总奖励:

可以使用许多深度学习软件包轻松计算策略梯度。 例如,这是 TensorFlow 的部分代码:

是的,通常情况下,编码看起来比解释更简单。
7、使用高斯策略进行连续控制
我们如何建立连续控制模型?
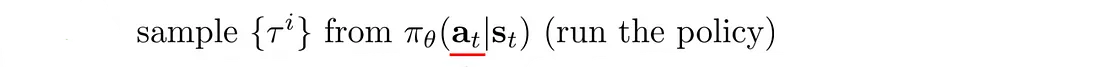
假设动作的值是高斯分布的:
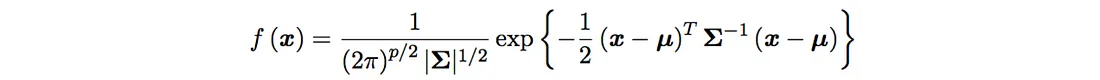
该策略是使用高斯分布定义的,其平均值是根据深度网络计算得出的:
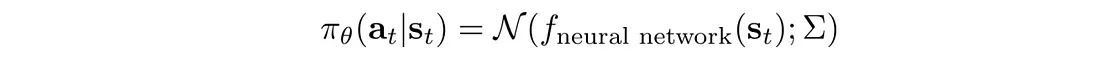
以及:
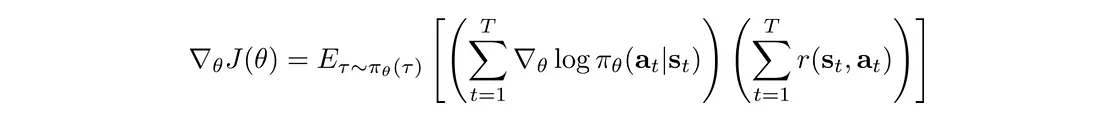
我们可以将 log π 的偏微分计算为:
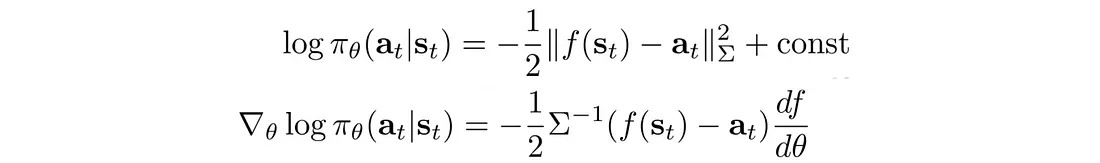
所以我们可以反向传播:
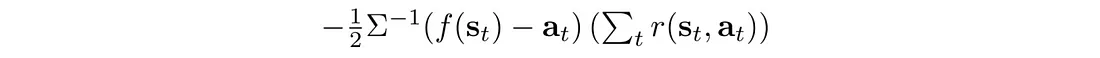
通过策略网络π来更新策略θ。 该算法看起来与以前完全相同。 只需以稍微不同的方式开始计算策略的对数即可:

8、策略梯度改进
策略梯度存在高方差和低收敛性的问题。
蒙特卡洛播放整个轨迹并记录轨迹的确切奖励。 然而,随机政策可能在不同时期采取不同的行动。 一个小转弯就可以完全改变结果。 所以蒙特卡罗没有偏差(bias),但方差(variance)很高。 方差会损害深度学习优化。 方差为模型学习提供了冲突的下降方向。 一个采样的奖励可能想要增加对数可能性,而另一个采样的奖励可能想要减少它。 这会损害收敛性。 为了减少由动作引起的方差,我们希望减少采样奖励的方差。
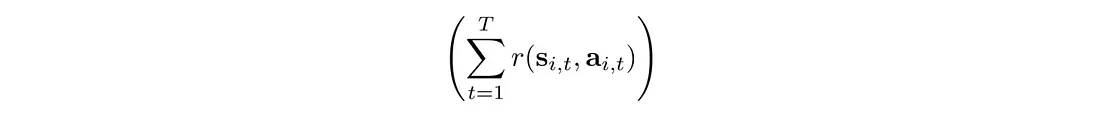
增加 PG 中的批大小可以减少方差。
然而,增加批大小会显着降低样本效率。 所以我们不能将其增加太多,我们需要额外的机制来减少方差。
8.1 基线
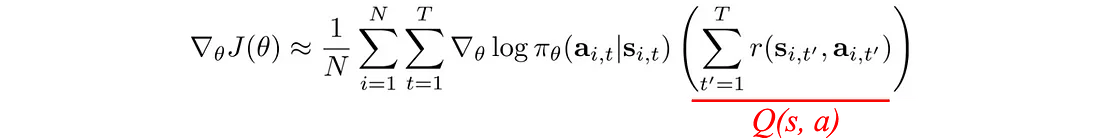
我们可以在优化问题中减去一项,只要该项与 θ 无关。 因此,我们不使用总奖励,而是用 V(s) 减去它。
我们定义优势函数 A 并根据 A 重写策略梯度:
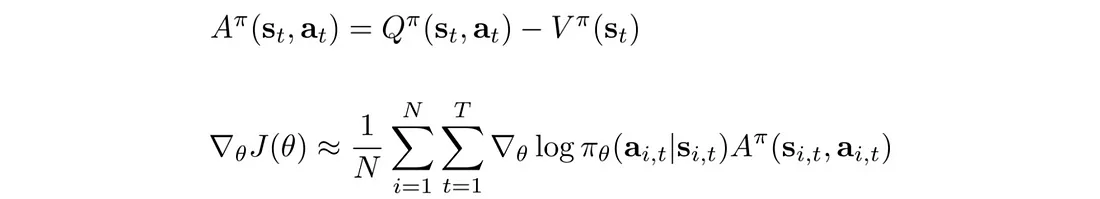
在深度学习中,我们希望输入特征以零为中心。 直观上,强化学习感兴趣的是了解某个动作是否执行得比平均值更好。 如果奖励总是正数(R>0),PG 总是尝试增加轨迹概率,即使它收到的奖励比其他人少得多。 考虑两种不同的情况:
- 情况1:轨迹A获得+10奖励,轨迹B获得-10奖励。
- 情况2:轨迹A获得+10奖励,轨迹B获得+1奖励。
在第一种情况下,PG会增加轨迹A的概率,同时减少B的概率。在第二种情况下,它将增加两者。 作为人类,我们可能会降低这两种情况下轨迹 B 的可能性。
通过引入 V 这样的基线,我们可以重新调整相对于平均动作的奖励。
8.2 普通策略梯度算法
这是使用基线 b 的策略梯度算法的通用算法。
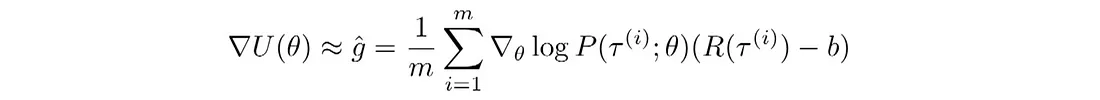

8.3 因果性
未来的行动不应改变过去的决定。 当前的行动只会影响未来。 因此,我们可以改变我们的目标函数来反映这一点:
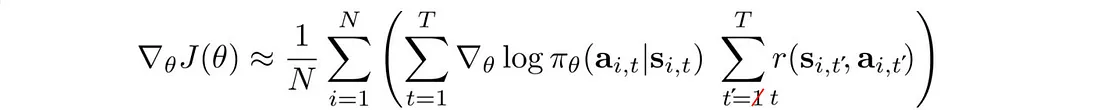
8.4 奖励折扣
奖励折扣减少了差异,从而减少了远期操作的影响。 这里,使用不同的公式来计算总奖励:
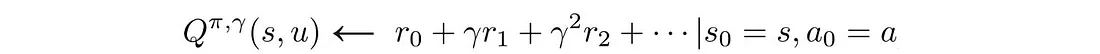
相应的目标函数变为:
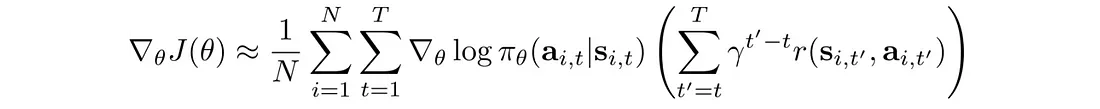
原文链接:RL — Policy Gradient Explained
BimAnt翻译整理,转载请标明出处





