NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模
在这篇博文中,我将介绍一种查找曲线拐点的方法。 一个简单的理解方式:将曲线想象成我们正在行驶的道路,我们想要找到我们停止右转并开始左转或反之的点,如下所示:
我们将展示解决方案的草图和 PostGIS 中的实际实施。 我认为这是一个很好的展示在数据库中实现 GIS 算法的有用技术的简单示例。
1、解决方案的草图
这个问题可以用非常标准的二维计算几何资源来解决。 特别是,使用叉积作为检测点位于给定直线左侧还是右侧的方法在这里很有用。 以下伪代码基于行列式:
function isLeft(Point a, Point b, Point c){
return ((b.X - a.X)*(c.Y - a.Y) - (b.Y - a.Y)*(c.X - a.X)) > 0;
}总的来说,我反对实现你自己的计算几何代码:数学公式的直接翻译通常会遇到舍入错误、极端情况和明显的低效率问题。 你最好使用优秀的计算几何库之一,例如:GEOS,它最初是作为 JTS 的一个移植,或 CGAL。 无论如何你都可能在使用它们,因为它们位于许多 GIS 软件堆栈的底部。 这适用于任何非平凡的数学(线性代数、优化……)。 记住:浮点数不是实数。
在这种情况下,我更关心实用性而不是纯粹的效率,使用 SQLs 数字类型以牺牲速度为代价提供任意精度的算术,防止了我们在双精度时会遇到的一些舍入错误,节省了 我们自己实施快速健壮的谓词。
2、PostGIS 实现
长期以来,我一直认为 Postgres/PostGIS 是地理空间分析的最佳工作台(证明我错了)。 在许多用例中,能够直接在存储数据的地方执行分析是无与伦比的。 必须编写 SQL 脚本对于某些用户来说可能是一种倒退,但在数据工作流的可重现性和可追溯性方面很有用。
在这种特殊情况下,我们假设我们的输入是一个包含 LineString 几何特征的表格,每个几何特征都有其唯一标识符。 当然,在任何计算之前,都会对几何图形进行适当的索引和有效性测试。 在开发过程中,通过感兴趣的区域将计算限制在数据的子集内,以缩短测试结果和参数的迭代过程也很有用。
解决方案的草图是:
- 简化几何结构以避免噪声(误报)。 ST_Simplify 或 ST_SimplifyPreserveTopology 就足够了。
- 分解点,跟踪原始几何图形,这可以使用 generate_series 和 ST_DumpPoints 轻松完成。
- 我们需要 3 个点来计算 isLeft:2 个来定义段,1个是要测试的点。 因此,对于沿 LineString 的每个点,我们得到该点本身和前 2 个点的 X、Y 坐标。 我们将检查当前点相对于前两个点定义的线段的位置。 这也意味着当检测到转折点时,将是该段的最后一个点,即:前一个点。 我发现通过 Posgres 窗口函数这个计算出奇的简单。
- 使用以上几点来计算 isLeft 的度量。
- 选择此度量更改的点。
像往常一样,良好的代码实践通常也适用于数据库。 特别是,CTE 可用于阐明查询,就像在任何编程语言中命名变量或函数一样:以实现重用,同时通过提供描述性名称来增强可读性。 任何在该语言中通常被认为是正常的令人眼花缭乱的 SQL 查询都没有任何借口。
查看草图解决方案并与以下实现进行对比以了解我的意思:
WITH
-- Optional: area of interest.
aoi AS (
SELECT ST_SetSRID(
ST_MakeBox2D(
ST_Point(467399,4671999),
ST_Point(470200,4674000))
,25831)
AS geom
),
-- Simplify geometries to avoid excessive noise. Tolerance is empiric and depends on application
simplified AS (
SELECT oid as contour_id, ST_Simplify(input_contours.geom, 0.2) AS geom
FROM input_contours, aoi
WHERE input_contours.geom && aoi.geom
),
-- Explode points generating index and keeping track of original curve
points AS (
SELECT contour_id,
generate_series(1, st_numpoints(geom)) AS npoint,
(ST_DumpPoints(geom)).geom AS geom
FROM simplified
),
-- Get the numeric values for X an Y of the current point
coords AS (
SELECT *, st_x(geom)::numeric AS cx, st_y(geom)::numeric AS cy
FROM points
ORDER BY contour_id, npoint
),
-- Add the values of the 2 previous points inside the same linestring
-- LAG and PARTITION BY do all the work here.
segments AS (
SELECT *,
LAG(geom, 1) over (PARTITION BY contour_id) AS prev_geom,
LAG(cx::numeric, 2) over (PARTITION BY contour_id) AS ax,
LAG(cy::numeric, 2) over (PARTITION BY contour_id) AS ay,
LAG(cx::numeric, 1) over (PARTITION BY contour_id) AS bx,
LAG(cy::numeric, 1) over (PARTITION BY contour_id) AS by
FROM coords
ORDER BY contour_id, npoint
),
det AS (
SELECT *,
(((bx-ax)*(cy-ay)) - ((by-ay)*(cx-ax))) AS det -- cross product in 2d
FROM segments
),
-- Uses the SIGN multipliaction as a proxy for XOR (change in convexity)
convexity AS (
SELECT *,
SIGN(det) * SIGN(lag(det, 1) OVER (PARTITION BY contour_id))
AS change
FROM det
)
SELECT contour_id, npoint, prev_geom AS geom
FROM convexity
WHERE change = -1
ORDER BY contour_id, npoint以下是示例区域的结果:
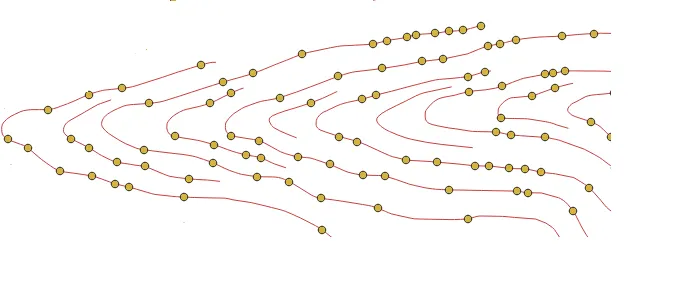
原文链接:Finding Curve Inflection Points in PostGIS
BimAnt翻译整理,转载请标明出处





