NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模
轴旋转角是表示实体 3D 对象旋转的一种可能方式。 其他表示有:四元数、矩阵和欧拉角。
1、旋转表示
旋转可以用单位向量和围绕该向量的旋转角度来表示。
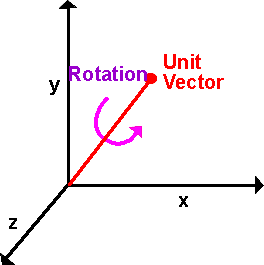
任何 3D 旋转都可以用这种方式表示,换句话说,给定一个方向为 1 的实体对象和具有不同方向 2 的同一对象。然后我们总能找到一个轴和角度,从方向 1 旋转到方向 2。
哪个旋转方向为正? 在这个网站上,我们将使用右手法则。
Axis-Angle 可能是我们指定 3D 旋转最容易理解的方法之一。 但是,请注意,3D 旋转在某些方面可能违反直觉(请参阅页面右侧的框)。 使用轴角表示 3D 旋转的一个缺点是我们不能直接组合两个旋转来给出等效的总旋转,为此我们需要使用矩阵或四元数,四元数与轴角相关,因此它不太难转换 它们之间的解释在这里。 另一个缺点是在 0° 和 180° 处有两个奇点,其中轴可能会突然跳转以进行微小的输入变化。
我们还可以使用轴和角度来表示任何瞬时角速度,如此处所述。
2、泛化到其他维数
一维空间中的旋转:我们不能在一维空间中旋转,因此不适用。
二维空间中的旋转:我们只需要角度,不需要轴,因为我们只有一个平面可以旋转。
3 维空间中的旋转:如本页其余部分所述。
在 4 维或更多维空间中旋转:
任何旋转都可以通过将对象投影到二维平面上然后将其旋转一个角度来表示。 平面可以用双矢量定义。碰巧,在三维空间中,双矢量是三维的,在这种情况下,平面(由双矢量表示)和线(由矢量表示)是对偶的。 这意味着,在三维空间中,我们可以用一条称为轴的线来表示旋转方向。 这很有用,因为它可以更直观地表示绕轴而不是平面的旋转方向。
原文链接:Maths - Axis Angle
BimAnt翻译整理,转载请标明出处





