NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模
本文是处理多边形和网格的各种笔记和算法。
1、表面简化
下面描述了一种方法,用于减少构成表面表示的多边形数量,同时仍试图保留表面的基本形式。 如果正在为渲染和/或交互环境寻求性能改进,那么此应用程序是显而易见的。
基本方法是重复删除具有最短共享边的多边形。 每一步移除两个多边形,剩余多边形的顶点移动到短边的中点。

以下示例说明了球体的小平面表示法。 初始球体有 4000 个面,每次迭代时多边形的数量减少 1000。初始球体显然效率低下,首先,有些区域比其他区域(例如:极点)更详细。 如果使用平滑的阴影渲染,那么具有 1000 个面的模型可能与具有 4 倍面数的原始模型一样好。
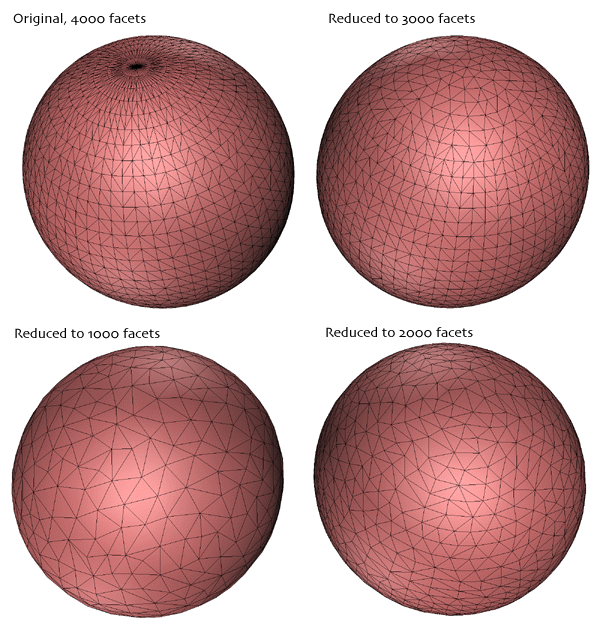
正如预期的那样,由于多边形数量的严重减少,表面会变得平滑并丢失细节。 对于网格立方体,这很容易说明。
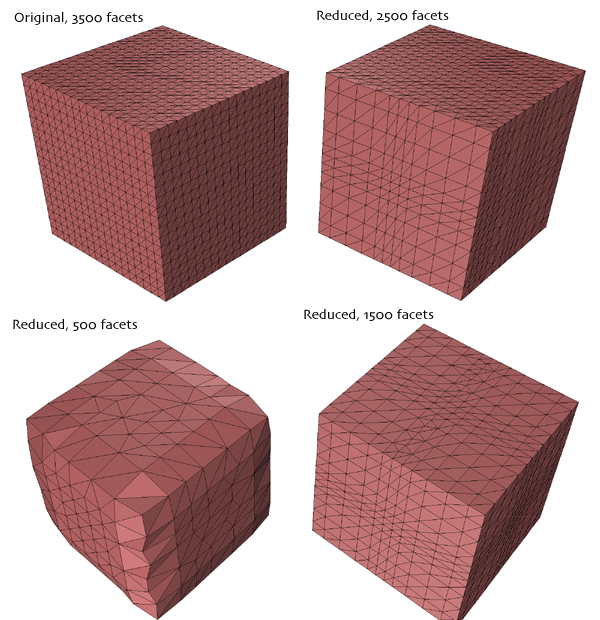
需要仔细考虑非流形表面的边缘。 当最短的小平面边缘位于表面的边缘时,一个简单的实现将慢慢吞噬边缘。

最后,应用于人类皮层模型。
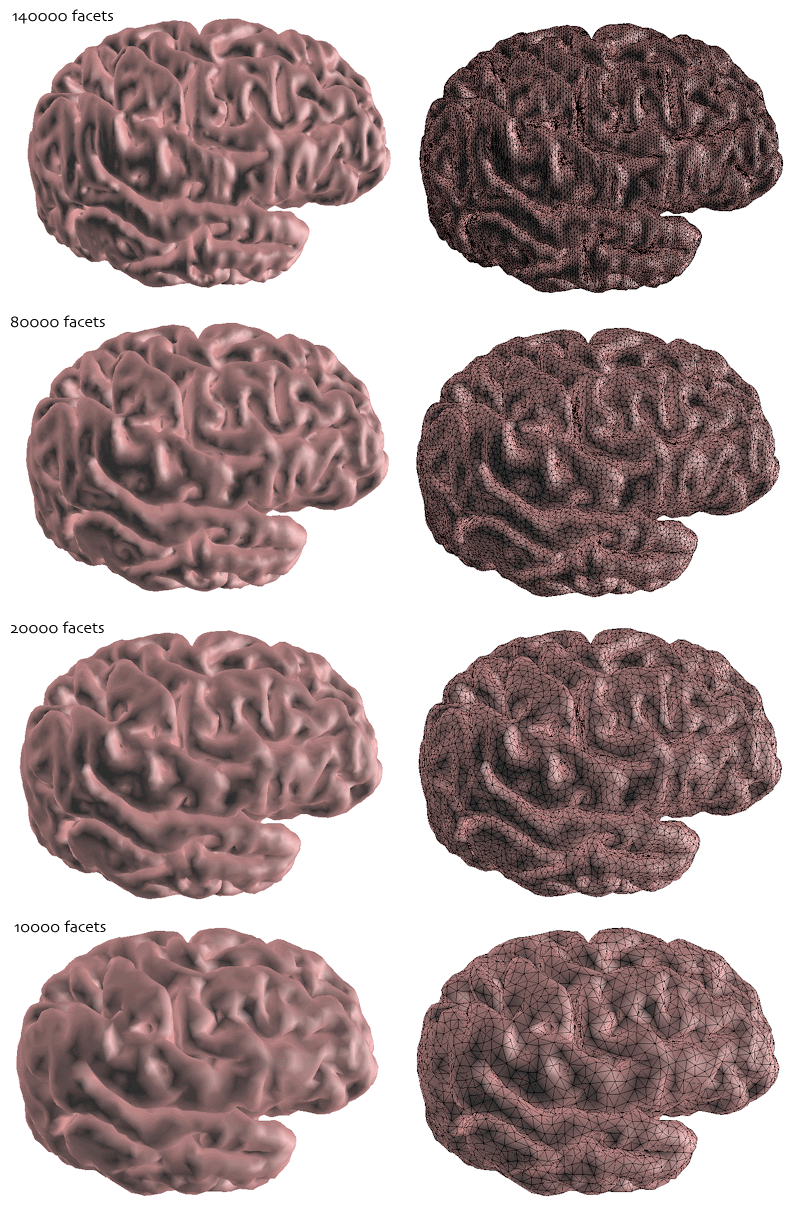
2、用任意平面裁剪多边形面
这个笔记连同末尾的源代码通过任意平面裁剪一个 3 顶点的面。 小平面由其 3 个顶点描述,裁剪平面由其法线和平面上的一个点指定。 平面的裁剪面被认为是包含法线的那一面,在下图中,这是裁剪面的右侧。
平面的标准方程是
A x + B y + C z + D = 0其中 (A,B,C) 是单位法线。 D的值由代入平面上的已知点 (Px,Py,Pz)确定,即
D = - (A Px + B Py + C Pz)对于顶点 (Qx,Qy,Qz) 表达式
side(Q) = A Qx + B Qy + C Qz + D可用于确定顶点位于平面的哪一侧。 如果为正,则点位于法线的同一侧,如果为负,则位于另一侧,如果为零,则位于平面上。
在确定边是否与切割平面相交后,有必要计算交点,因为该交点将成为剪裁面的顶点。 令边在两点 P0 和 P1 之间,沿线段的点的方程
P = P0 + u(P1 - P0)其中 u 介于 0 和 1 之间。将其代入平面的表达式
A (P0x + u (P1x - P0x)) + B (P0y + u (P1y - P0y)) + C (P0z + u (P1z - P0z)) + D = 0求解u:
u = - side(P0) / (side(P1) - side(P0))将其代入直线方程给出实际的交点。
有 8 种不同的情况需要考虑,它们在下表中进行了说明,并按顺序出现在源代码中。 前两种情况是所有点都在裁剪平面的任一侧。 左边三种情况是平面的裁剪边只有一个顶点的情况,右边三种情况是平面的裁剪边有两个顶点的情况。
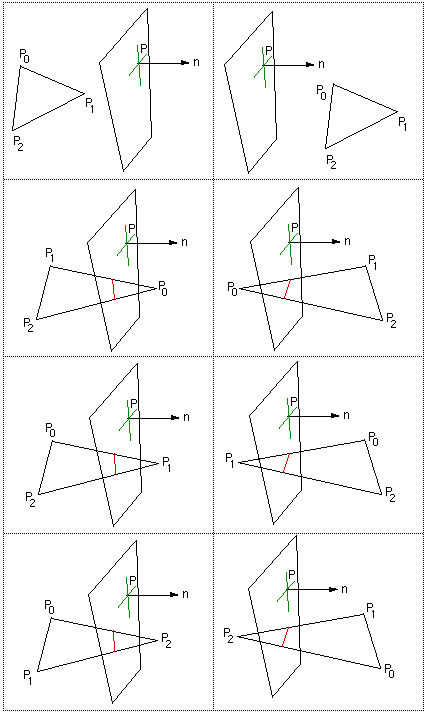
注意:
- 当裁剪侧只有一个点时,生成的面有 4 个顶点,如果底层数据库只处理 3 个顶点面,则可以使用多种方法将其一分为二。
- 当要裁剪的面有 3 个以上的顶点时,可以先细分它们,然后单独裁剪每个片段。
所提出的算法没有被零除的问题 - 这里的C源代码进行了适当的裁剪,当平面的裁剪侧有一个点时,计算顶点的顺序对于 3 种情况很重要。
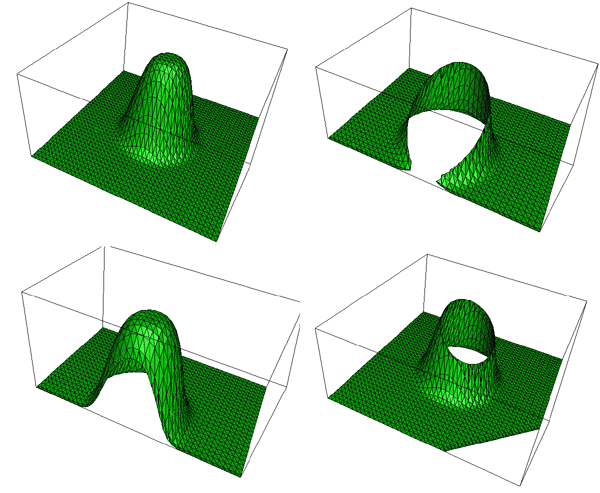
作为示例和测试练习,以下显示了二维高斯分布和三个裁剪平面的结果。
3、表面松弛和平滑
本文档描述了一种平滑由平面集合描述的一般表面的方法。 小平面不需要均匀分布,也不需要位于网格上,它们可以形成任意的 3D 表面。 可以迭代地应用该方法以将表面平滑到任意程度。 一般而言,该方法试图保留粗略的特征,并且往往会产生大小相等的刻面(通常是理想的特征)。 这种通用技术通常称为表面松弛。
考虑一个由 n 个顶点 Pj 包围的点 Pi,这些顶点构成共享顶点 Pi 的面。
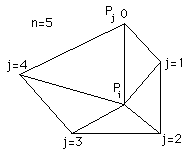
然后点 Pi 被扰动如下:
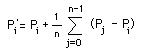
作为示例,请考虑下面的顶部图,它是一个二维高斯分布,每个顶点的每个 x、y、z 分量都添加了噪声。 随后的平滑版本是分别迭代应用该技术 1、2、3 和 6 次的结果。
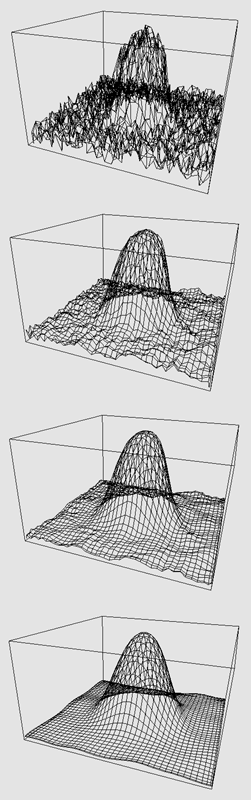
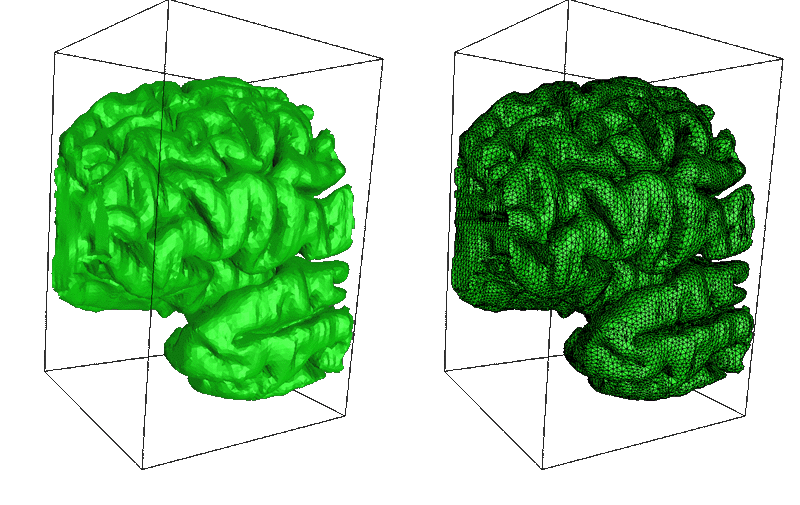
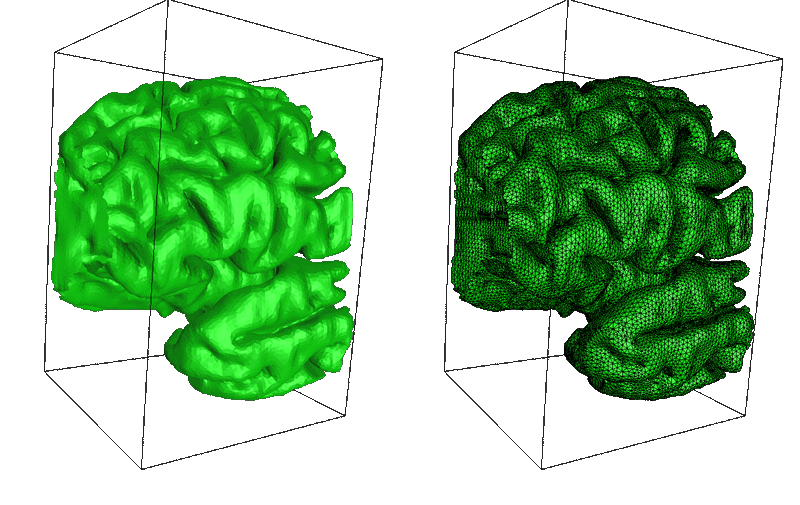
下面是一个更“真实”的例子,特别是,刻面不是排列在简单的网格上,而是大小不一。 几何形状是来自人类皮层模型的 2 厘米切片。 左侧的原始表面具有清晰的垂直棱纹,这是由于对略微未对齐的扫描图像进行数字化处理而产生的。 右侧的表面应用了一次松弛迭代。 垂直伪影明显减少。

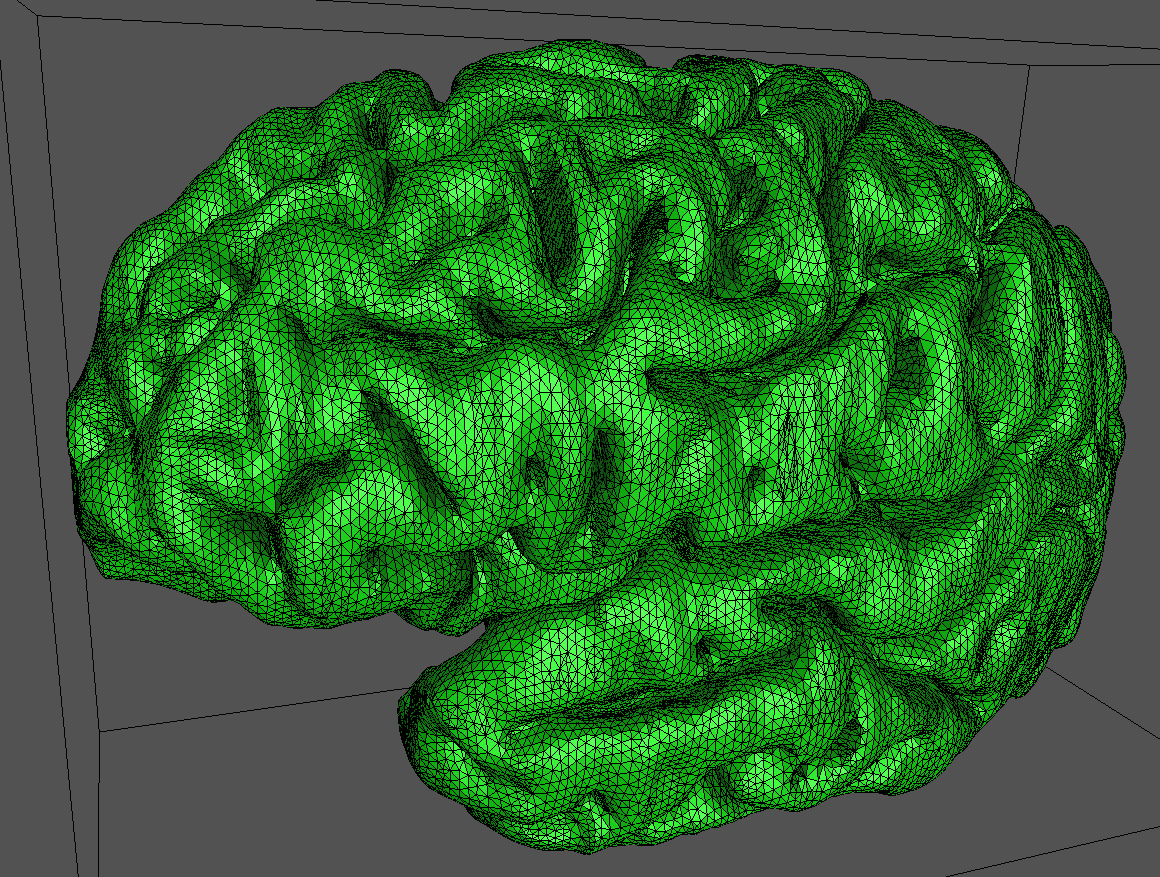
下面显示了同一模型通过两次松弛迭代的不同切片。 这对图像是相同的,只是小平面边缘绘制在右侧的表面上。 在这两种情况下,表面都是使用平面着色渲染的,也就是说,没有跨小平面进行平滑处理。

4、几何褶皱
在大多数渲染应用程序中,可以使用所谓的纹理贴图或更准确地说是凹凸贴图来模拟粗糙表面。 这些图像会在渲染过程中扰乱表面法线,从而产生粗糙表面的外观或凸起和降低的结构,例如瓷砖地板中的灌浆。
在某些情况下,希望以几何方式实际表示表面粗糙度。 例如,当从很近的地方观看时,许多纹理不会保留其所需的效果。 有些效果也很难使用凹凸贴图生成,例如,变形的范围有限。
根据确切的效果,有多种修改几何体的方法。 一个效果是起皱,就像您对一张纸所做的那样。 在以下示例中,每个分面都被拆分为 3x3 网格。 然后将每个顶点置换一个随机量(高斯分布)。 当然,对于每个位移,共享该顶点的所有小平面也会被修改。

上图显示了揉皱运动前后的 Menger 海绵。
有几点需要注意
- 这整个过程至少可以说是低效的。 在这种情况下,几何内容几乎增加了 10 倍。
- 4 点面一般不再共面,即使它们在原始模型中,对这些进行三角测量进一步增加了几何内容。
- 如果不希望面相交,则位移的范围是有限的。
5、分裂面
下面讨论将基于面的计算机模型拆分成更小的面的多种方法。 想要这样做的原因有很多,其中包括:
- 为了给表面添加细节,例如,分形空间细分
- 用于表面松弛算法
- 消除会导致某些渲染和纹理算法出现问题的窄角面
| Method | Additional Geometry | Comments |
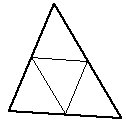 | Increases the number of facets by 3 | Perhaps the most common splitting technique. Doesn't result in finer internal angles. |
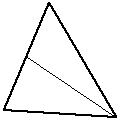 | Doubles the number of facets | Simplest method, bisection. Normally the longest edge or the widest internal angle would be bisected. While it reduces long edges it also tends to produce narrow internal angles |
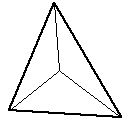 | 2 additional facets | The centroid becomes the new vertex. If the facet is part of a height field the centroid height would normally be the average of the 3 original vertex heights. |
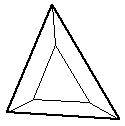 | Results in an identical but smaller triangular facet and three new 4 vertex facets. | Uncommon |
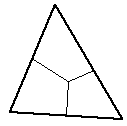 | Yields three 4 vertex facets. | The centroid is usually used as the mid point. |
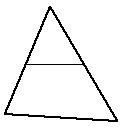 | Gives a smaller 3 point facet and a new 4 point facet. | This is a common first approach for long thin facets, the cut is made along the two longest edges |
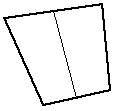 | Subdivide a 4 point facet into two 4 point facets | Simple example of a more general repeated bisection of a facet. The longest opposite pair of edges are split if equal size facets are desirable. |
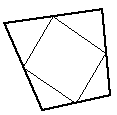 | Results in a small 4 point facet and four new triangular facets. | Uncommon |
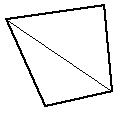 | Bisection into two triangular facets | The simplest splitting of a 4 point facet. Most commonly used by rendering program to ensure all facets are planar. Results in facets with small internal angles. |
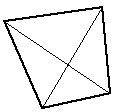 | Gives three triangular facets. | The centroid is normally used. An improved technique to simple bisection for smoothing height fields. |
6、小平面、平面、法线、渲染
在计算机图形应用程序中表示有界平面(小平面)的常用方法是作为顶点序列。 着色算法和光线追踪通常需要了解小平面的法线,这是通过对小平面的边缘向量进行叉积计算得出的。 法线与光源矢量所成的角度决定了小平面的阴影程度。 特别是,如果法线指向光源,则表面被明亮地照亮,如果法线背向光源,则表面处于阴影中。
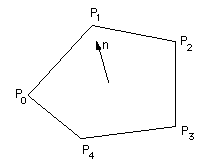
一个常见的问题出现了,因为顶点需要以特定的顺序指定。 一个共同的惯例是需要对它们进行排序,使法线指向外部。 这假设有一个“外部”和“内部”,即:对象是封闭的。
计算法线和光源向量之间夹角的常用方法包括取这两个向量之间的叉积,得到它们之间夹角的余弦值。 一些渲染包简单地使用这个角度的绝对值,从而使背面的阴影与面向光源的一侧相同。
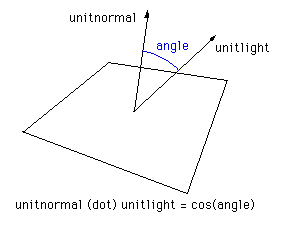
当你无法控制面的来源或渲染包时,另一种常见的技术是将每个面加倍,副本的顶点顺序相反。 这两个侧面显然可以组成不封闭的物体。
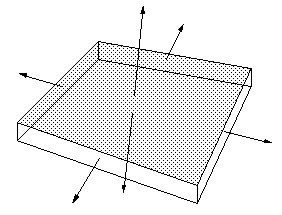
出现基本问题是因为小平面/平面在现实生活中不存在,所有平面的厚度都是有限的。 这类似于在光线追踪包中表示线条的问题……它们必须变成具有有限厚度的物体,例如圆柱体。 在建筑建模中创建具有有限厚度的平面已被认可很长时间,其中从无限薄的平面创建墙壁会导致各种问题,如果使用它们的真实厚度则不会遇到。
7、多边形类型
在计算机建模和图形中有许多常用的多边形类别。 使用的特定多边形类型会对许多渲染和编辑算法的复杂性产生巨大影响。 例如,用于将多边形拆分为多个 3 个顶点面的算法对于凸多边形来说是微不足道的,而对于有孔的多边形来说则问题很大。
虽然大部分讨论将关于多边形作为 3D 中的有界平面,但同样的想法也适用于 2D 中的多边形。
下面将列出和讨论一些更常用的类别。
- 3顶点面
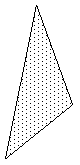
这是最简单的多边形类型。 也许最重要的特征之一是点位于平面上,因此它通常是 3D 渲染应用程序的最基本基元,这些应用程序期望整个多边形区域有一个明确的法线。
- 矩形面
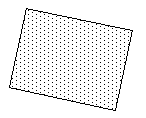
矩形或 4 顶点多边形是从网格数据集和二维表面的多边形近似生成的。 许多自然出现这种矩形面的应用程序不能确保顶点共面,幸运的是将这样的多边形变成三角形并因此变成平面多边形是微不足道的。
- 凸多边形
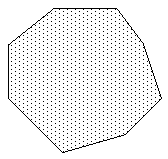
这是具有 3 个或 4 个以上顶点的最简单的多边形类型。
- 凹多边形
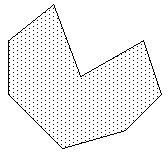
这是最普遍的“简单”多边形类型,即没有孔。
- 复杂多边形
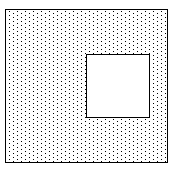
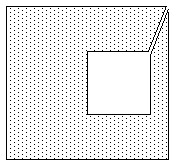
有孔的多边形有多种定义方式。 孔可以这样“标记”,一种常见的方法是以不同于实体部分的顺序定义孔的顶点。 例如,实心部分可能围绕法线顺时针定义,孔洞围绕法线逆时针定义。
通过在实心多边形和孔多边形之间引入 2 条重合边,可以将此类多边形变成凹多边形。 对于多个孔和凹形实体块,需要在适当的顶点之间取重合边,以避免形成重叠的多边形。
- 相交多边形
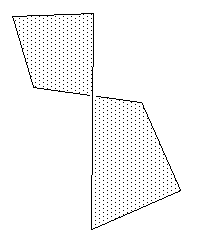
这些有点反常的多边形通常会与带孔的复杂多边形混为一谈。上边的例子是最直接的情况,多边形覆盖自身一部分的情况通常会被避免,并且渲染引擎不会一致地处理。
8、确定多边形顶点是顺时针还是逆时针排列
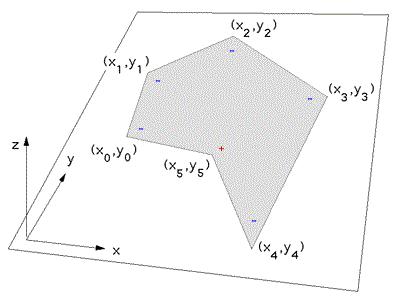
下面分别介绍凸多边形和凹多边形判断多边形的顶点顺序是顺时针还是逆时针的方法。 假设多边形由 N 个有序顶点描述:
(x0,y0), (x1,y1), (x2,y2), . . . (xn-1,yn-1)凸多边形的顶点排序的简单测试是基于相邻边之间叉积的考虑。 如果叉积为正,则它上升到平面上方(z 轴向上超出平面),如果为负,则叉积进入平面。
cross product = ((xi - xi-1),(yi - yi-1)) x ((xi+1 - xi),(yi+1 - yi))
= (xi - xi-1) * (yi+1 - yi) - (yi - yi-1) * (xi+1 - xi)正叉积意味着我们有一个逆时针多边形。
要确定凹多边形的顶点顺序,可以使用多边形面积计算的结果,其中面积由下式给出:
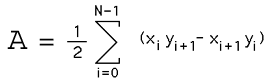
如果上述表达式为正,则多边形按逆时针方向排序,否则,如果为负,则多边形顶点按顺时针方向排序。
- 测试凹/凸多边形
对于凸多边形,所有相邻边的叉积符号相同,对于凹多边形,叉积符号混合。
源代码:
9、将线段剪裁成复杂的多边形
下面介绍将线段裁剪成复杂多边形的过程。 复杂多边形是指凹多边形和有孔的多边形。
无论要求是保留多边形内的那部分线还是移除多边形内的多边形部分,概念都是相同的。
考虑两点 P1 和 P2 之间的线段的参数表达式:
P = P1 + mu (P2 - P1) where 0 <= mu <= 1然后可以计算出这条线段与多边形边的所有交点。
通过增加沿直线的 mu 值来排列这些交点。 这些点在多边形内部和外部交替形成边对:
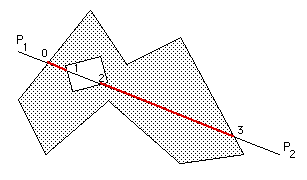
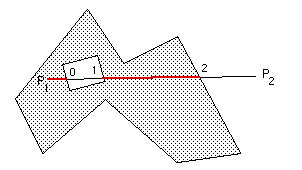
唯一剩下的歧义是线段 (mu = 0) 的第一个点 P1 是在多边形内还是在多边形外,有关详细信息,请参见此处。
9、计算 3D 多边形的面积
- 三角形面的面积
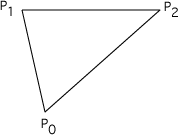
这完全源于叉积的定义:
A = || (P1 - P0) x (P2 - P0) || / 2- 四面体的面积(假设是平面)
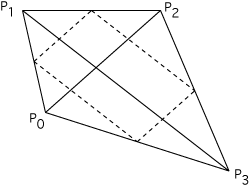
这个比较有意思,留给读者的练习是4条边的中点连成的四边形是平行四边形,而且四边形的面积是这个平行四边形面积的一半。 有关更多信息,请参阅 Pierre Varignon,他在 1730 年左右发现了这一点。
A = || (P2 - P0) x (P3 - P1) || / 2- 任意平面多边形的面积
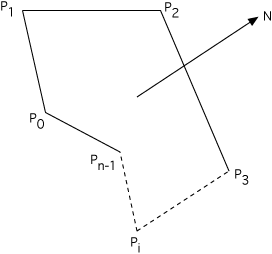
这种一般情况在某种程度上更难推导出来。 一种方法是 Stokes 定理,另一种方法是将多边形分解为三角形或四边形。 在下面的 N 是多边形所在平面的法线。
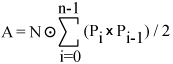
10、确定一个点是否位于多边形的内部
- 解决方案 1 (2D)
以下是计算机图形学中经常遇到的问题的简单解决方案,确定点 (x,y) 是否位于二维多边形边界平面的内部或外部。 这在诸如光栅设备上的多边形填充、绘图软件中的阴影以及确定多个多边形的交集等应用中是必需的。
考虑一个由 N 个顶点 (xi,yi) 组成的多边形,其中 i 的范围从 0 到 N-1。 假定最后一个顶点 (xN,yN) 与第一个顶点 (x0,y0) 相同,即多边形是闭合的。 要确定点 (xp,yp) 的状态,请考虑从 (xp,yp) 向右发出的水平射线。 如果这条射线与构成多边形的线段相交的次数是偶数,则该点在多边形之外。 而如果交叉点的数量是奇数,则点 (xp,yp) 位于多边形内。 下面显示了一些样本点的射线,应该使技术清楚。
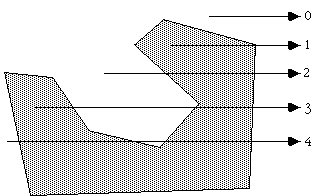
注意:出于本次讨论的目的,0 将被视为偶数,偶数或奇数的测试将基于模数 2,即如果交点数模数 2 为 0 则该数为偶数,如果为 1 则该数为偶数 这很奇怪。
唯一的技巧是在多边形的边或顶点位于来自 (xp,yp) 的射线上时发生的特殊情况。 可能的情况如下图所示。
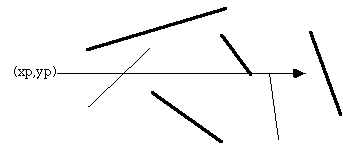
上面的粗线不被视为有效交叉点,细线确实算作交叉点。 忽略沿射线的边缘或终止于射线的边缘的情况确保端点仅被计算一次。
请注意,此算法也适用于有孔的多边形,如下图所示:
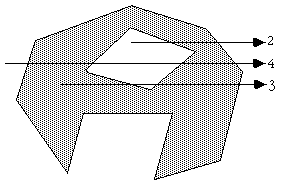
以下 C 函数返回 INSIDE 或 OUTSIDE,指示点 P 相对于具有 N 个点的多边形的状态:
#define MIN(x,y) (x < y ? x : y)
#define MAX(x,y) (x > y ? x : y)
#define INSIDE 0
#define OUTSIDE 1
typedef struct {
double x,y;
} Point;
int InsidePolygon(Point *polygon,int N,Point p)
{
int counter = 0;
int i;
double xinters;
Point p1,p2;
p1 = polygon[0];
for (i=1;i<=N;i++) {
p2 = polygon[i % N];
if (p.y > MIN(p1.y,p2.y)) {
if (p.y <= MAX(p1.y,p2.y)) {
if (p.x <= MAX(p1.x,p2.x)) {
if (p1.y != p2.y) {
xinters = (p.y-p1.y)*(p2.x-p1.x)/(p2.y-p1.y)+p1.x;
if (p1.x == p2.x || p.x <= xinters)
counter++;
}
}
}
}
p1 = p2;
}
if (counter % 2 == 0)
return(OUTSIDE);
else
return(INSIDE);
}以下代码由 Randolph Franklin 编写,它为内部点返回 1,为外部点返回 0。
int pnpoly(int npol, float *xp, float *yp, float x, float y)
{
int i, j, c = 0;
for (i = 0, j = npol-1; i < npol; j = i++) {
if ((((yp[i] <= y) && (y < yp[j])) ||
((yp[j] <= y) && (y < yp[i]))) &&
(x < (xp[j] - xp[i]) * (y - yp[i]) / (yp[j] - yp[i]) + xp[i]))
c = !c;
}
return c;
}Alexander Motrichuk 的贡献:InsidePolygonWithBounds.cpp。
“对于上面的大多数算法,如果被查询的点恰好位于顶点上,就会出现病态情况。解决这个问题的最简单方法是将其作为一个单独的过程进行测试,并自行决定是否需要 在内部或外部考虑它们。”
Giuseppe Iaria 在 VBA 中的贡献:InsidePolygon.txt
Jerry Knauss 用 c# 编写的贡献:contains.c#。
- 解决方案 2 (2D)
Philippe Reverdy 提出的另一个解决方案是计算测试点与构成多边形的每对点之间的角度之和。 如果这个和是 2pi 那么这个点是一个内点,如果是 0 那么这个点是一个外点。 这也适用于带孔的多边形,因为多边形是使用由重合边进出孔组成的路径定义的,这是许多 CAD 软件包中的常见做法。
然后可以在 C 中将内部/外部测试定义为:
typedef struct {
int h,v;
} Point;
int InsidePolygon(Point *polygon,int n,Point p)
{
int i;
double angle=0;
Point p1,p2;
for (i=0;i<n;i++) {
p1.h = polygon[i].h - p.h;
p1.v = polygon[i].v - p.v;
p2.h = polygon[(i+1)%n].h - p.h;
p2.v = polygon[(i+1)%n].v - p.v;
angle += Angle2D(p1.h,p1.v,p2.h,p2.v);
}
if (ABS(angle) < PI)
return(FALSE);
else
return(TRUE);
}
/*
Return the angle between two vectors on a plane
The angle is from vector 1 to vector 2, positive anticlockwise
The result is between -pi -> pi
*/
double Angle2D(double x1, double y1, double x2, double y2)
{
double dtheta,theta1,theta2;
theta1 = atan2(y1,x1);
theta2 = atan2(y2,x2);
dtheta = theta2 - theta1;
while (dtheta > PI)
dtheta -= TWOPI;
while (dtheta < -PI)
dtheta += TWOPI;
return(dtheta);
}- 解决方案 3 (2D)
对于具有特殊属性的多边形,此问题还有其他解决方案。 如果多边形是凸的,那么可以将多边形视为从第一个顶点开始的“路径”。 如果一个点始终位于构成路径的所有线段的同一侧,则该点位于该多边形的内部。
给定 P0 (x0,y0) 和 P1 (x1,y1) 之间的线段,另一个点 P (x,y) 与线段具有以下关系。
计算:
(y - y0) (x1 - x0) - (x - x0) (y1 - y0)如果它小于 0 则 P 在线段的右侧,如果大于 0 则在线段的左侧,如果等于 0 则它在线段上。
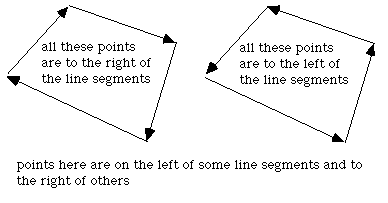
- 解决方案 4 (3D)
该解决方案的动机是解决方案 2 以及与 Reinier van Vliet 和 Remco Lam 的通信。 要确定一个点是否在 3D 凸多边形的内部,人们可能会首先确定该点是否在平面上,然后确定它的内部状态。 这两个都可以通过计算测试点(下面的 q)和每对边缘点 p[i]->p[i+1] 之间的角度之和来一次性完成。 如果点都在多边形的平面上并且在内部,则此总和仅为 2pi。 离多边形点q越远,角度和趋于0。
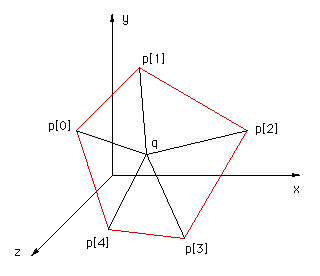
以下代码片段返回测试点 q 与所有顶点对之间的角度和。 请注意,角度和以弧度返回。
typedef struct {
double x,y,z;
} XYZ;
#define EPSILON 0.0000001
#define MODULUS(p) (sqrt(p.x*p.x + p.y*p.y + p.z*p.z))
#define TWOPI 6.283185307179586476925287
#define RTOD 57.2957795
double CalcAngleSum(XYZ q,XYZ *p,int n)
{
int i;
double m1,m2;
double anglesum=0,costheta;
XYZ p1,p2;
for (i=0;i<n;i++) {
p1.x = p[i].x - q.x;
p1.y = p[i].y - q.y;
p1.z = p[i].z - q.z;
p2.x = p[(i+1)%n].x - q.x;
p2.y = p[(i+1)%n].y - q.y;
p2.z = p[(i+1)%n].z - q.z;
m1 = MODULUS(p1);
m2 = MODULUS(p2);
if (m1*m2 <= EPSILON)
return(TWOPI); /* We are on a node, consider this inside */
else
costheta = (p1.x*p2.x + p1.y*p2.y + p1.z*p2.z) / (m1*m2);
anglesum += acos(costheta);
}
return(anglesum);
}注意:对于上面的大多数算法,如果要查询的点恰好位于顶点上,则存在病态情况。 解决这个问题的最简单方法是将其作为一个单独的过程进行测试,并自行决定是否要在内部或外部考虑它们。
11、计算多边形的面积和质心
- 面积
确定多边形面积的问题充其量看起来很混乱,但最终的公式却特别简单。 结果和示例源代码 (C) 将在此处提供。 考虑由 N 个顶点 (xi,yi) 之间的线段组成的多边形,i=0 到 N-1。 假定最后一个顶点 (xN,yN) 与第一个顶点相同,即:多边形是闭合的。
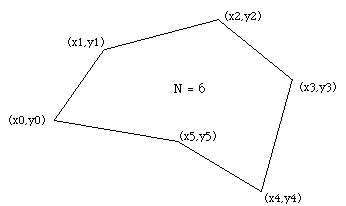
面积由以下公式给出:
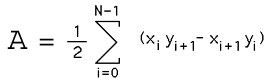
注意带孔的多边形。 通常通过在与孔的方向相反的方向上对封闭多边形的顶点进行排序来定义孔。 该算法仍然有效,只是在将多边形面积与所有孔的面积相加后取绝对值。 也就是说,孔区域将与边界多边形区域的符号相反。
上面的面积表达式的符号(没有绝对值)可以用来确定多边形顶点的顺序。 如果符号为正,则多边形顶点围绕法线逆时针排列,否则顺时针排列。
要得出此解决方案,请从每个顶点投影线到多边形最低部分下方的水平线。 每条线段的封闭区域由三角形和矩形组成。 将这些区域加在一起,注意当多边形循环到开头时,多边形外部的区域最终会取消。
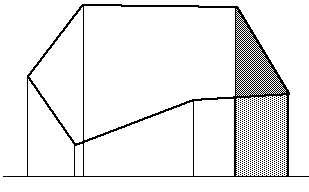
要使此技术起作用,将对多边形施加的唯一限制是多边形不能自相交,例如,在以下情况下解决方案将失败。
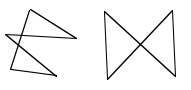
- 质心
质心也称为“重心”或“质心”。 假设多边形由密度均匀的材料制成,质心的位置如下所示。 与上面面积的计算一样,假定 xN 为 x0,换句话说,多边形是封闭的。
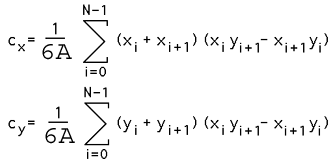
- 由 3 个顶点面描述的 3D 壳的质心
下面给出了由具有顶点 (ai,bi,ci) 的 N 个三角形面的集合组成的 3D 对象的质心 C。 Ri 是第 i 个面的顶点的平均值,Ai 是第 i 个面面积的两倍。 请注意,假设这些面是质量均匀的薄片,它们不需要连接或形成一个实体对象。 对于 2D 3 顶点多边形,这减少到上面的等式。
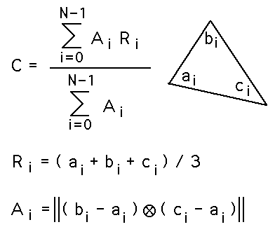
- 多边形的二阶矩
下面假设逆时针方向的多边形顶点,顺时针方向的多边形使用负值。
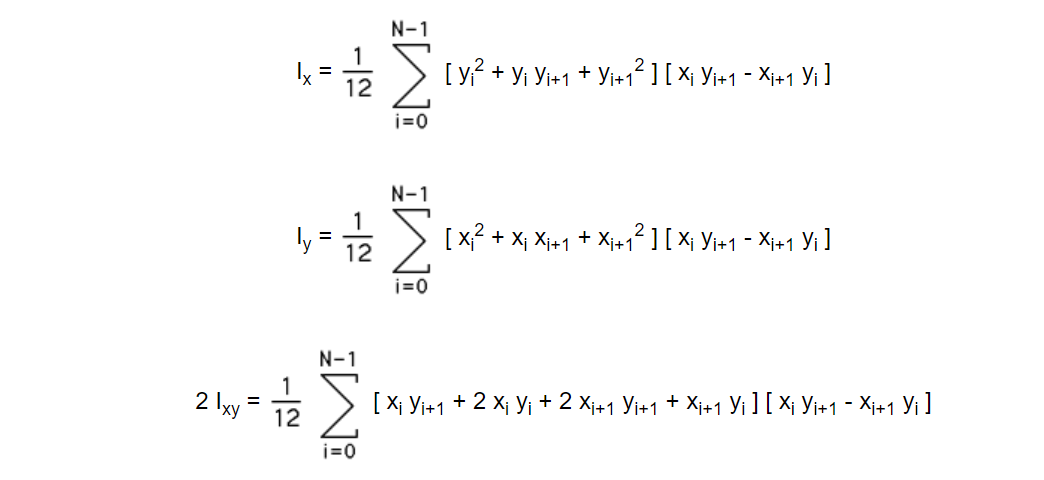
示例源代码
- 此 C 函数返回多边形的面积。
- VBA 版本由 Rui Vaz Rodrigues 提供
- Ramón Talavera 提交的 JAVA 代码。
- PolygonUtilities.java 由 Christopher Fuhrman 贡献
- Rodrigo Alves Pons 的 Pascal/Dephi 示例。
- Basic版本也由 Rodrigo Alves Pons 设计。
- Raymond Hill 的 JavaScript。
- Python 版本和示例由 Jorg Rødscø提供。
12、确定线段是否与 3 顶点面相交
以下将找到线段和平面 3 顶点面之间的交点(如果存在)。 数学和解决方案还可以用于找到平面和线之间的交点,这是一个更简单的问题。 可以通过首先将它们三角化为多个 3 顶点面来找到更复杂的多边形之间的交集。
源代码将在最后提供,它说明了解决方案,而不是为了提高效率而编写。 线段和面的标注和命名约定如下图所示:
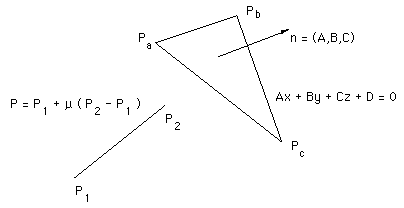
该过程将在给定由其两个端点定义的线段和由其三个顶点界定的小平面的情况下实施。
该解决方案包括以下步骤:
- 检查直线和平面是否平行
- 找到给定线段所在的线与包含小平面的平面的交点
- 检查交点是否位于线段上
- 检查交点是否位于小平面内
通过将直线 P = P1 + mu (P2 - P1) 的方程式代入平面 Ax + By + Cz + D = 0 的方程式中找到交点 P。
请注意,A、B、C 的值是平面法线的分量,可以通过取任意两个归一化边缘向量的叉积来找到,例如:
(A,B,C) = (Pb - Pa) cross (Pc - Pa)然后通过将一个顶点代入平面的方程中找到 D 例如:
A Pax + B Pay + C Paz = -D这给出了 mu 的表达式,从中可以使用直线方程找到交点 P。
mu = ( D + A P1x + B P1y + C P1z ) / ( A (P1x - P2x) + B (P1y - P2y) + C (P1z - P2z) )如果上面的分母为 0,则直线平行于平面并且它们不相交。 对于位于线段上的交点,mu 必须介于 0 和 1 之间。
最后,我们需要检查交点是否位于由 Pa、Pb、Pc 界定的平面内
这里使用的方法依赖于一个事实,即三角形内部点的内角和为 2pi,三角形小平面外的点将具有较小的内角和。
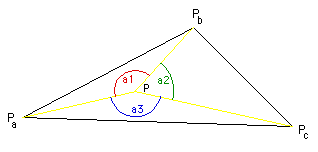
如果我们按如下方式形成单位向量 Pa1、Pa2、Pa3(P 是要测试的点,看它是否在内部)
Pa1 = (Pa - P) / |(Pa - P)|
Pa2 = (Pb - P) / |(Pb - P)|
Pa3 = (Pc - P) / |(Pc - P)|角度是
a1 = acos(Pa1 dot Pa2)
a2 = acos(Pa2 dot Pa3)
a3 = acos(Pa3 dot Pa1)源代码
/*
Determine whether or not the line segment p1,p2
Intersects the 3 vertex facet bounded by pa,pb,pc
Return true/false and the intersection point p
The equation of the line is p = p1 + mu (p2 - p1)
The equation of the plane is a x + b y + c z + d = 0
n.x x + n.y y + n.z z + d = 0
*/
int LineFacet(p1,p2,pa,pb,pc,p)
XYZ p1,p2,pa,pb,pc,*p;
{
double d;
double a1,a2,a3;
double total,denom,mu;
XYZ n,pa1,pa2,pa3;
/* Calculate the parameters for the plane */
n.x = (pb.y - pa.y)*(pc.z - pa.z) - (pb.z - pa.z)*(pc.y - pa.y);
n.y = (pb.z - pa.z)*(pc.x - pa.x) - (pb.x - pa.x)*(pc.z - pa.z);
n.z = (pb.x - pa.x)*(pc.y - pa.y) - (pb.y - pa.y)*(pc.x - pa.x);
Normalise(&n);
d = - n.x * pa.x - n.y * pa.y - n.z * pa.z;
/* Calculate the position on the line that intersects the plane */
denom = n.x * (p2.x - p1.x) + n.y * (p2.y - p1.y) + n.z * (p2.z - p1.z);
if (ABS(denom) < EPS) /* Line and plane don't intersect */
return(FALSE);
mu = - (d + n.x * p1.x + n.y * p1.y + n.z * p1.z) / denom;
p->x = p1.x + mu * (p2.x - p1.x);
p->y = p1.y + mu * (p2.y - p1.y);
p->z = p1.z + mu * (p2.z - p1.z);
if (mu < 0 || mu > 1) /* Intersection not along line segment */
return(FALSE);
/* Determine whether or not the intersection point is bounded by pa,pb,pc */
pa1.x = pa.x - p->x;
pa1.y = pa.y - p->y;
pa1.z = pa.z - p->z;
Normalise(&pa1);
pa2.x = pb.x - p->x;
pa2.y = pb.y - p->y;
pa2.z = pb.z - p->z;
Normalise(&pa2);
pa3.x = pc.x - p->x;
pa3.y = pc.y - p->y;
pa3.z = pc.z - p->z;
Normalise(&pa3);
a1 = pa1.x*pa2.x + pa1.y*pa2.y + pa1.z*pa2.z;
a2 = pa2.x*pa3.x + pa2.y*pa3.y + pa2.z*pa3.z;
a3 = pa3.x*pa1.x + pa3.y*pa1.y + pa3.z*pa1.z;
total = (acos(a1) + acos(a2) + acos(a3)) * RTOD;
if (ABS(total - 360) > EPS)
return(FALSE);
return(TRUE);
}13、欧拉数和封闭曲面
由根据边和顶点定义的平面多边形组成的几何图形的欧拉数是:
V-E+F其中 V、E 和 F 分别是顶点数、边数和面数。
对于封闭曲面,欧拉数始终等于 2。
这形成了对计算机生成的小平面几何形状闭合的简单测试。
14、将多边形分解为三角形的“EAR”方法
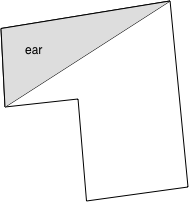
所谓的“ear clipping”算法是一种将简单的多边形(没有孔或交叉点)分解为一组三角形部分的方法。 “ear”被定义为一个三角形,其中两条边位于多边形边界上,第三条边包含在多边形内。 该方法依赖于双耳定理,即任何简单的多边形(多于 3 条边)至少由 2 个耳朵组成。 请注意,多边形不需要是 2D,但如果是 3D,则顶点必须全部位于一个平面上。 多边形可以具有凹陷部分。
下面的多边形显示的耳朵示例。 请注意,这个特定的多边形共有 5 个耳朵。
反复剪耳分解的过程如下图。 请注意,创建三角形的确切顺序和形状取决于发现耳朵的顺序。

原文链接:Polygons and meshes
BimAnt翻译整理,转载请标明出处





