光追加速之BVH层级包围体

NSDT工具推荐： Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模

在本章中，我们将介绍并使用由研究人员 Kay 和 Kajiya 于 1986 年开发的技术。 自那时以来的其他加速结构已被证明比他们的技术更好，但他们的解决方案可以帮助制定大多数加速结构的构建原则。 这是一个非常好的起点，就像犹他茶壶一样，我们将有机会介绍一些出现在许多其他计算机图形算法（例如八叉树结构）中的一些新的有趣的技术。 我们强烈建议你阅读他们的论文（查看本课末尾的参考文献部分）。

1、范围

在上一章中，我们直观地展示了可以使用诸如针对包围体的光线追踪之类的简单技术来加速光线追踪。 正如 Kay 和 Kajiya 在他们的论文中指出的那样，只有当光线追踪这些边界体积或范围（他们称之为边界体积或范围）比光线追踪对象本身快得多时，这些技术才有效。 他们还指出，如果范围松散地适合物体，那么与该包围体相交的许多光线实际上可能会错过内部的物体。

另一方面，如果范围精确地描述了对象，则与该范围相交的所有光线也将与该对象相交。 显然，符合这个标准的包围体就是物体本身。 因此，对于包围体来说，一个好的选择是在紧密度（范围与对象的贴合程度）和速度（复杂的包围体对于光线追踪而言比简单的形状更昂贵）之间提供良好权衡的形状。 这个想法如图 1 所示，其中茶壶周围的盒子比下图中茶壶周围更紧密的边界体积更快地进行光线追踪。 然而，与更紧密地拟合模型的范围相比，更多与该盒子相交的光线将错过茶壶几何形状。 在大多数情况下，诸如球体和盒子之类的形状会给出一些相当不错的结果，但利用在简单性和速度之间找到良好折衷的想法，Kay 和 Kajiya 提议进一步完善这些简单的形状。

边界框可以看作是彼此相交的平面。 为了使演示更容易，我们只考虑二维情况。 假设我们需要计算茶壶的边界框。 从技术上讲，这可以视为平行于 y 轴的两个平面与平行于 x 轴的两个平面的交集（图 2）。 我们现在需要找到一种计算这个平面的方法？ 我们该怎么做呢？ 我们已经在第 7 课中介绍了平面方程来计算射线与长方体的交点，并在第 9 课中介绍了计算射线与三角形的交点。 让我们回想一下，平面方程（这次是三维）可以定义为：

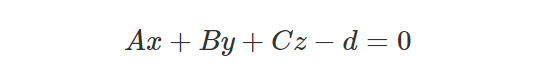
其中 A、B、C 定义平面的法线（垂直于平面的向量）并且d是沿该向量从世界原点到该平面的距离。 x、y、z 定义平面上点的 3D 笛卡尔坐标。 该方程表示，位于其坐标乘以平面法线坐标的位置上的任何点，减去d等于零。 该方程还可用于将茶壶的顶点投影到平面上并找到d的值。对于给定点Pxyz和一个给定的法线平面Nxyz，
我们可以求解d：

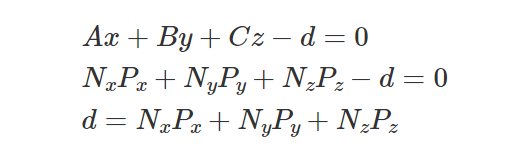
我们可以将该方程重写为更传统的点矩阵乘法形式（方程 1）：

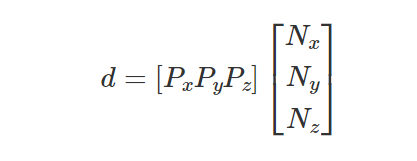
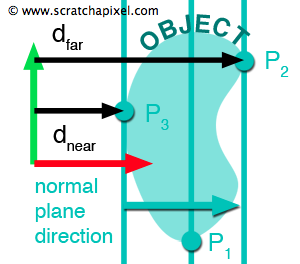
如果我们投影一个顶点Pxyz在具有法线N1,0,0的平面上, d给出沿 x 轴从原点到平行于 y 轴的平面的距离。 如果我们对模型的所有顶点重复此过程，我们可以表明具有最小d值的点和最大d值的点，分别对应于对象x坐标最小和最大范围。 这两个值dnear和dfar描述限制物体的两个平面（如图 3 所示）。 我们可以用下面的伪代码来实现这个过程：

// plane normal
vector N(1, 0, 0);
float Dnear = INFINITY;
float Dfar = -INFINITY;
for (each point in model) {
    // project point
    float D = N.x * P.x + N.y * P.y + N.z * P.z;
    Dnear = min(D, Dnear);
    Dfar = max(D, Dfar); 
}

在他们的论文中，Kay 和 Kajiya 将两个平面之间的空间区域称为板，定义板方向的法线向量称为平面集法线。 正如他们所观察到的：

平面设置法线的不同选择会产生对象的不同边界板。 一组边界板的交集产生边界体积。 为了在 3 空间中创建闭合包围体，必须至少涉及三个包围板，并且必须选择它们以便定义法向量跨越 3 空间。

此原理最简单的示例是轴对齐边界框 (AABB)，它由分别平行于 xz、yz 和 xy 平面的三个板定义（图 4）。 然而，Kay 和 Kajiya 建议不仅使用三个板，而是使用七个板来获得更紧密的边界体积。 这些板的平面设置法线是预先选择的，并且与要界定的对象无关。 为了更好地直观地了解其工作原理，让我们再次回到二维情况。 让我们想象一下用于绑定对象的平面集法线是：

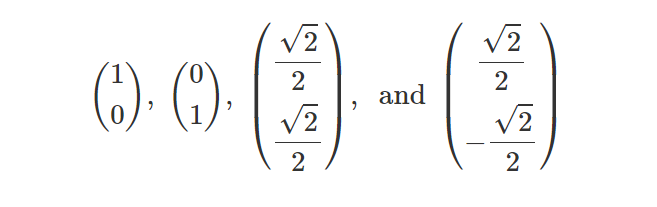
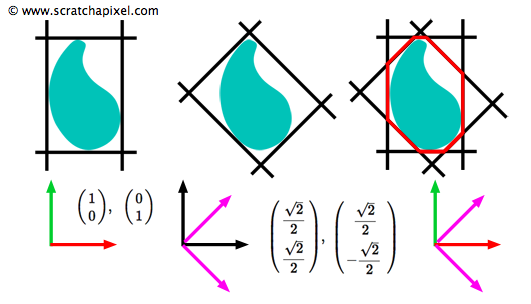
图 5 显示了由这些预先选择的平面设置法线包围的对象（这是 Kay 和 Kajiya 论文中图 3 的复制品）。

正如你所看到的，生成的边界框比简单的边界框更适合对象。 对于三维情况，他们使用七个平面集法线：

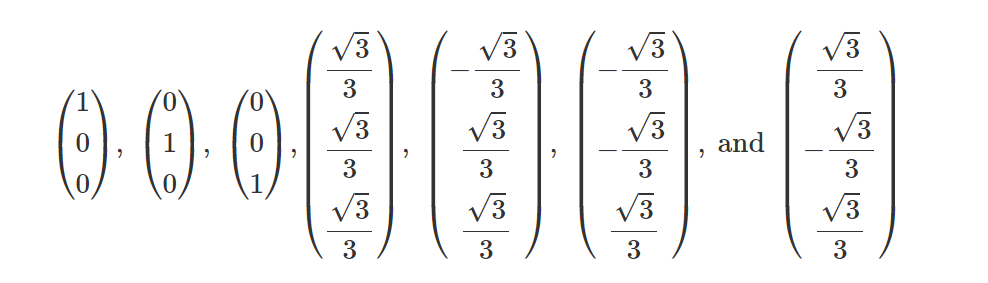
前三个平面集法线定义轴对齐的边界框，最后四个平面集法线定义八边平行六面体。 要构建对象的包围体积，我们只需找到以下值的最小值和最大值
对于每个板，通过将模型的顶点投影到七个平面集法线上。

2、射线-体块的交集

接下来，我们需要编写一些代码来对体块进行光线追踪。 其原理与光线盒相交的原理非常相似。 板由两个彼此平行的平面定义，如果光线不平行于这些平面，它将与它们相交，产生两个值tmin和tfar。为计算交叉点距离t，我们简单地将射线方程

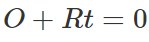
代入平面方程：

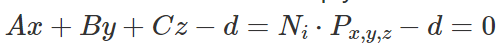
得到等式 2：

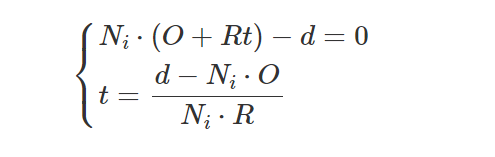
其中Ni是七个平面集法线之一，O和R分别是射线的原点和方向，d是从世界原点到法线平面的距离。Ni.O和Ni.R可以重新用于计算交叉点距离t。 对每个平面替换预先计算的值dnear和dfar：

// computing intersection of a given ray with slab
float NdotO = N . O;
float NdotR = N . R;
float tNear = (dNear - NdotO) / NdotR;
float tFar = (dFar - NdotO) / NdotR;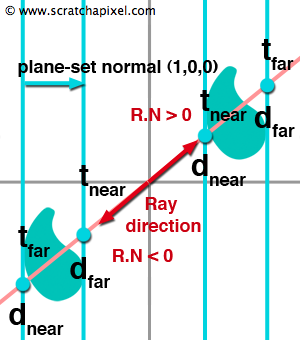

与盒子的光线追踪一样，当分母Ni.R接近于零时要小心。 此外，当分母小于零时，我们还需要交换dnear和dfar（见图 6）。 至于光线盒相交（有关算法的更多信息，请参阅第 7 课），针对包围对象的每个板执行此测试。 我们将保留最大的tnear值和最小的tfar。 如果最终的tfar大于tnear，那么标明光线与体块相交。 如果射线与体块相交，则t值指示这些交点沿射线的位置。 结果间隔（定义为tnear和tfar）对于估计物体沿射线的位置很有用。 现在让我们尝试将所学到的知识付诸实践。

3、源代码

以下 C++ 代码实现了本章中描述的方法。 BVH 类派生自 AccelerationStructure 基类。 我们在此类中创建一个名为 Extents 的结构，其中包含以下值dnear和dfar
对于所有七个预定义的平面设置法线（第 7-11 行）。

class BVH : public AccelerationStructure
{
    static const uint8_t kNumPlaneSetNormals = 7;
    static const Vec3f planeSetNormals[kNumPlaneSetNormals];
    struct Extents
    {
        Extents()
        {
            for (uint8_t i = 0; i < kNumPlaneSetNormals; ++i)
                d[i][0] = kInfinity, d[i][1] = -kInfinity;
        }
        bool intersect(const Ray<float> &ray, float &tNear, float &tFar, uint8_t &planeIndex);
        float d[kNumPlaneSetNormals][2];
    };
    Extents *extents;
public:
    BVH(const RenderContext *rcx);
    const Object* intersect(const Ray<float> &ray, IsectData &isectData) const;
    ~BVH();
};

在类的构造函数中，我们分配一个范围数组来存储场景中所有对象的包围体数据（第 3 行）。 然后，我们循环所有对象并调用 Object 类中的computeBounds 方法来计算包围该对象的每个板的值 dNear 和 dFar（第 4-8 行）。 在下面的代码片段中，我们仅显示 PolygonMesh 类的此函数。 我们遍历网格的所有顶点并将它们投影到当前平面上（第 27-31 行）。 类构造函数中完成的工作到此结束。

BVH::BVH(const RenderContext *rcx) : AccelerationStructure(rcx), extents(NULL) 
{ 
    extents = new Extents[rcx->objects.size()]; 
    for (uint32_t i = 0; i < rcx->objects.size(); ++i) { 
        for (uint8_t j = 0; j < kNumPlaneSetNormals; ++j) { 
            rcx->objects[i]->computeBounds(planeSetNormals[j], extents[i].d[j][0], extents[i].d[j][1]); 
        } 
    } 
} 

const Vec3f BVH::planeSetNormals[BVH::kNumPlaneSetNormals] = { 
    Vec3f(1, 0, 0), 
    Vec3f(0, 1, 0), 
    Vec3f(0, 0, 1), 
    Vec3f( sqrtf(3) / 3.f,  sqrtf(3) / 3.f, sqrtf(3) / 3.f), 
    Vec3f(-sqrtf(3) / 3.f,  sqrtf(3) / 3.f, sqrtf(3) / 3.f), 
    Vec3f(-sqrtf(3) / 3.f, -sqrtf(3) / 3.f, sqrtf(3) / 3.f), 
    Vec3f( sqrtf(3) / 3.f, -sqrtf(3) / 3.f, sqrtf(3) / 3.f) }; 
} 

class PolygonMesh : public Object 
{ 
    ... 
    void computeBounds(const Vec3f &planeNormal, float &dnear, float &dfar) const 
	{ 
        float d; 
        for (uint32_t i = 0; i < maxVertIndex; ++i) { 
            d = dot(planeNormal, P[i]); 
            if (d < dnear) dnear = d; 
            if (d > dfar) dfar = d; 
        } 
    } 
    ... 
}; 

一旦调用渲染函数，我们就调用 BVH 类的交集方法，而不是与场景的每个对象相交。 首先，针对场景中所有对象的所有包围体测试光线。 为此，我们从 Extent 结构中调用当前测试对象的体积数据的 intersect 方法（第 24 行）。 此方法只是计算当前光线与包围对象的七个板中每一个的交点，并跟踪最大的 dNear 值和最小的计算出的 dFar 值。 如果 dFar 大于 dFar，则与边界体积发生相交，并且函数返回 true。 在以下版本的代码中，如果射线与体积相交，我们将 IsectData 结构中的成员变量 N 设置为相交平面的法线。 该向量 N 与光线方向的点积结果用于设置当前像素的颜色。 生成的图像如图 7 所示。这有助于可视化相交和围绕对象的边界体积。

inline bool BVH::Extents::intersect(
	const Ray<float> &ray,
    float *precomputedNumerator, float
	*precomputeDenominator,
	float &tNear, float &tFar, uint8_t
	&planeIndex)
{
	for (uint8_t i = 0; i < kNumPlaneSetNormals; ++i) {
        float tn = (d[i][0] - precomputedNumerator[i]) / precomputeDenominator[i];
        float tf = (d[i][1] - precomputedNumerator[i]) / precomputeDenominator[i];
        if (precomputeDenominator[i] < 0) std::swap(tn, tf);
        if (tn > tNear) tNear = tn, planeIndex = i;
        if (tf < tFar) tFar = tf;
        if (tNear > tFar) return false;
    }
 
    return true;
}

const Object* BVH::intersect(const Ray<float> &ray, IsectData &isectData) const
{
	float tClosest = ray.tmax;
    Object *hitObject = NULL;
    float precomputedNumerator[BVH::kNumPlaneSetNormals], precomputeDenominator[BVH::kNumPlaneSetNormals];
    for (uint8_t i = 0; i < kNumPlaneSetNormals; ++i) {
        precomputedNumerator[i] = dot(planeSetNormals[i], ray.orig);
        precomputeDenominator[i] = dot(planeSetNormals[i], ray.dir);;
    }
    for (uint32_t i = 0; i < rc->objects.size(); ++i) {
        __sync_fetch_and_add(&numRayVolumeTests, 1);
        float tNear = -kInfinity, tFar = kInfinity;
        uint8_t planeIndex;
        if (extents[i].intersect(ray, precomputedNumerator, precomputeDenominator, tNear, tFar, planeIndex)) {
            if (tNear < tClosest)
                tClosest = tNear, isectData.N = planeSetNormals[planeIndex], hitObject = rc->objects[i];
        }
    }
 
    return hitObject;
}

但在 intersect 方法的以下最终版本中，如果边界体积相交，我们将测试射线与体积所包围的对象（或对象，例如三角形网格）之间是否存在相交 。 当测试成功时，如果相交距离是迄今为止我们找到的最小距离，我们会更新 tClosest 并保留指向相交对象的指针。

int main(int argc, char **argv)
{
    clock_t timeStart = clock();
    ...
    rc->accelStruct = new BVH(rc);//AccelerationStructure(rc);
    render(rc, filename);
    ...
    printf("Render time                                 : %04.2f (sec)\n", (float)(timeEnd - timeStart) / CLOCKS_PER_SEC);
    printf("Total number of triangles                   : %d\n", totalNumTris);
    printf("Total number of primary rays                : %llu\n", numPrimaryRays);
    printf("Total number of ray-triangles tests         : %llu\n", lrt::numRayTrianglesTests);
    printf("Total number of ray-triangles intersections : %llu\n", lrt::numRayTrianglesIsect);
    printf("Total number of ray-volume tests            : %llu\n", lrt::numRayBoxTests);
    return 0;
}

最后，如果我们使用新的加速结构编译并运行程序，我们会得到以下统计数据：

Render time                                 : 2.92 (sec)
Total number of triangles                   : 16384
Total number of primary rays                : 307200
Total number of ray-triangles tests         : 80998400
Total number of ray-triangles intersections : 111889
Total number of ray-volume tests            : 9830400

该技术比前一章的方法快 1.34 倍。 看起来似乎不多，但在简单场景中节省的几秒钟可能会在复杂场景中变成几个小时。

原文链接：Bounding Volume Hierarchy: BVH (part 1)

BimAnt翻译整理，转载请标明出处