NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模
要使基础的光栅化器正常工作,我们需要做的就是知道如何将三角形投影到屏幕上,将投影坐标转换为光栅空间,然后光栅化三角形,并可能使用深度缓冲区来解决可见性问题。 这已经足以创建 3D 场景的图像,这些图像既是透视正确的,又可以解决可见性问题(被其他对象隐藏的对象确实不会出现在应该遮挡它们的对象前面) )。 这已经是一个很好的结果了。 我们提供的用于执行此操作的代码是实用的,但可以大大优化; 然而,优化光栅化算法不是我们在本课中讨论的内容。
1、顶点属性插值的透视校正
那么,这一章我们要讨论什么呢? 在专门介绍光栅化的章节中,我们讨论了使用重心坐标来插值顶点数据或顶点属性(这是最常见的名称)。 当然,我们可以使用重心坐标来插值深度值,这是它们的主要功能之一,但它们也可以用于插值顶点属性。顶点属性在渲染中起着非常重要的作用,尤其是在光照和着色方面。 当我们在本节中讨论着色时,我们将提供有关如何在着色中使用顶点属性的更多信息。 但是你不需要了解任何有关着色的知识即可理解透视正确插值和顶点属性的概念。
你可能想知道为什么我们不在着色中讨论这个主题,如果它与更具体的着色相关。 顶点属性确实与着色更具体地相关,但透视正确插值的主题与光栅化的主题更具体地相关。
如你所知,我们需要将原始顶点(相机空间顶点)的 z 坐标存储在投影顶点(屏幕空间顶点)的 z 坐标中。 这是必需的,以便我们可以计算投影三角形表面上的点的深度。 正如上一章所述,深度是解决可见性问题所必需的,深度是通过使用重心坐标对三角形顶点 z 坐标的倒数进行线性插值来计算的。
相同的技术可用于插入我们想要的任何其他变量,只要该变量的值是在三角形的顶点定义的,类似于我们存储在投影点 z 坐标中的方式。 例如,在三角形顶点存储颜色是很常见的。 存储在三角形顶点的另外两个最常见的变量或属性(这是 CG 中的专有术语)是纹理坐标和法线。 纹理坐标是用于纹理化的 2D 坐标(我们将在本节中研究的技术)。 法线用于着色并定义表面的方向(查看有关着色的课程以了解有关法线和平滑着色的更多信息)。
在本文中,我们将更具体地使用颜色和纹理坐标来说明透视正确插值的问题。
2、透视校正的实现算法
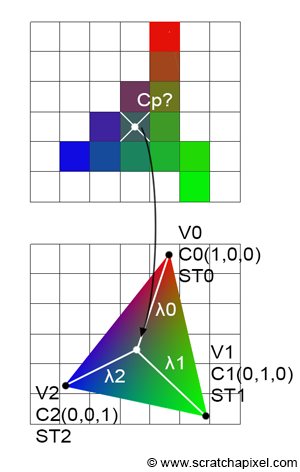
正如光栅化阶段一章中提到的,我们可以为三角形顶点指定颜色或任何其他我们想要的东西。 可以使用重心坐标对这些属性进行插值,以找出三角形内任何点的这些属性的值。 换句话说,在光栅化时,顶点属性必须在三角形的表面上进行插值。 流程如下:
- 你可以根据需要为三角形的顶点指定任意数量的顶点属性。 它们是在原始 3D 三角形(在相机空间中)上定义的。 在我们的示例中,我们将分配两个顶点属性,一个用于颜色,一个用于纹理坐标。
- 三角形被投影到屏幕上(三角形的顶点从相机空间转换为光栅空间)。
- 在屏幕空间中,三角形被“光栅化”。 如果像素与三角形重叠,则计算该像素的重心坐标。
- 在三角形角或顶点定义的颜色(或纹理坐标)使用先前计算的重心坐标进行插值,使用以下公式:
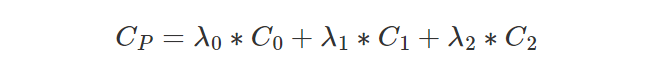
其中 λ0、λ1 和 λ2 是像素的重心坐标,C0、C1 和 C2 是三角形顶点的颜色。 结果 Cp 被分配给帧缓冲区中的当前像素。 可以执行相同的操作来计算像素重叠的三角形上的点的纹理坐标:
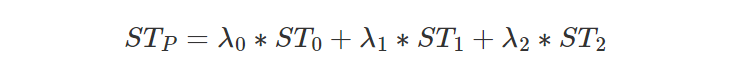
这些坐标用于纹理。
但这种技术根本行不通。 为了理解原因,让我们看看位于 3D 四边形中间的点会发生什么。 正如你在图 2 的顶视图中看到的,我们有一个四边形,点 P 显然位于该四边形的中间(P 位于四边形对角线的交点处):
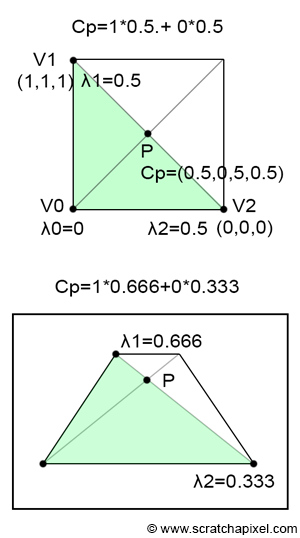
不过,当我们从随机的角度来看这个问题时,很容易看出,根据四边形相对于相机的方向,P 似乎不再位于四边形的中心。 这是由于透视投影如前所述保留了线条但不保留距离。 但请记住,重心坐标是在屏幕空间中计算的。 想象一下四边形是由两个三角形组成的。 在 3D 空间中,P 位于 V1-V2 之间的相等距离,因此在 3D 空间中其重心坐标为 (0,0.5,0.5)。 不过,在屏幕空间中,由于 P 距离 V1 比距离 V2 更近,因此 λ1 大于 λ2(且 λ0 等于 0)。 但问题是这些是用于插值三角形顶点属性的坐标。 如果 V1 为白色且 V2 为黑色,则 P 处的颜色应为 0.5。 但如果 λ1 大于 λ2,那么我们将得到一个大于 0.5 的值。 因此,显然我们用来插值顶点属性的技术不起作用。 我们假设如图 1 所示,λ1 和 λ2 分别等于 0.666 和 0.334。 如果我们对三角形的顶点颜色进行插值,我们会得到:
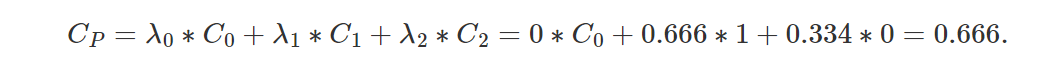
我们得到 P 颜色的 0.666,而不是我们应该得到的 0.5。 有一个问题,这个问题在某种程度上与我们在上一章中学到的有关顶点 z 坐标插值的知识有关。
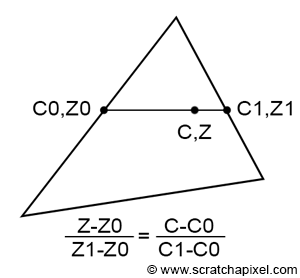
希望找到正确的解决方案并不难。 假设我们有一个三角形,三角形的每条边都有两个 z 坐标 Z0 和 Z1,如图 3 所示。如果我们连接这两个点,我们可以使用线性插值来插值这条线上的点的 z 坐标。 我们可以使用分别定义在三角形上与 Z0 和 Z1 相同的位置处的顶点属性 C0 和 C1 的两个值来执行相同的操作。 从技术上讲,由于 Z 和 C 都是使用线性插值计算的,因此我们可以写出以下等式(等式 1):
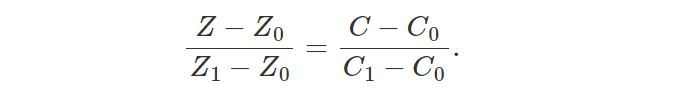
从上一章我们还知道(等式2):
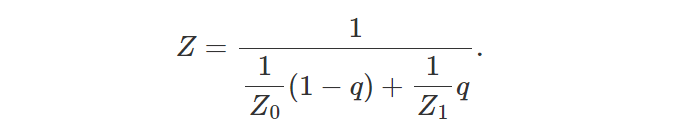
我们要做的第一件事是将方程 1 左侧的 Z(方程 2)代入方程。简化所得方程的技巧是将方程 2 的分子和分母乘以 Z0Z1 以消除 1/Z0 和 1/Z1 项:
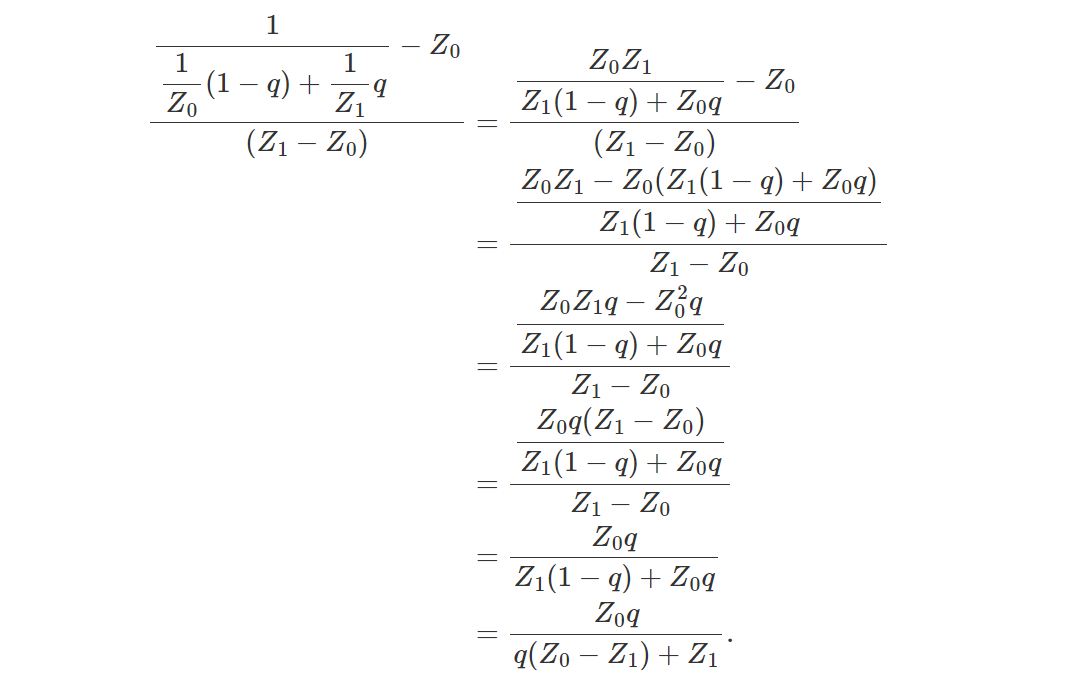
现在我们可以求解 C:
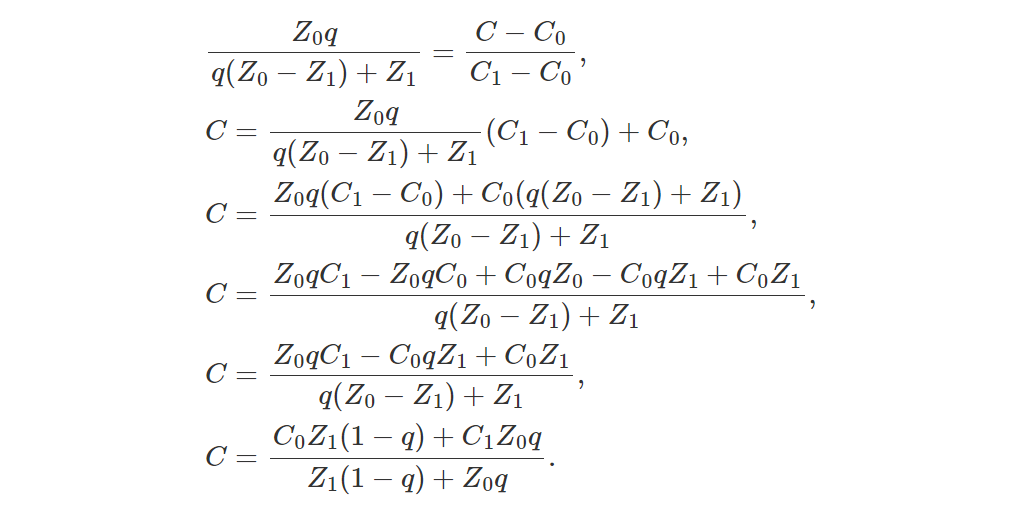
如果我们现在将分子和分母乘以 1/Z0Z1,我们就可以从方程右侧提取 Z 的因子:
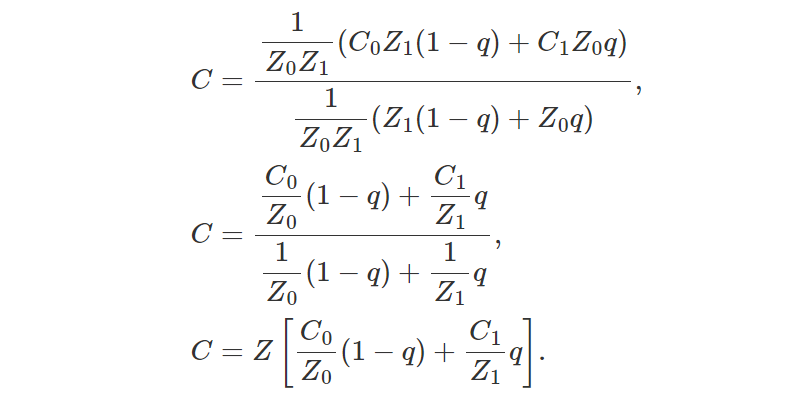
花了一段时间才得到这个结果,但这是光栅化中一个非常基本的方程(顺便说一句,它很少在任何地方得到解释。有时会解释,但很少提供得到该结果的步骤),因为它用于插值顶点属性是渲染中非常重要且常见的特征。
该方程表示,要正确插值顶点属性,我们首先需要将顶点属性值除以定义它的顶点的 z 坐标,然后使用 q 对其进行线性插值(在我们的例子中,将是 2D 三角形上像素的重心坐标),然后最后将结果乘以 Z,Z 是三角形上像素重叠的点的深度(相机空间中顶点属性被设置的点的深度) 插值。 这是我们在第三章中使用的代码的另一个版本,它显示了透视正确顶点属性插值的示例:
// compile with:
// c++ -o raster3d raster3d.cpp
// for naive vertex attribute interpolation and:
// c++ -o raster3d raster3d.cpp -D PERSP_CORRECT
// for perspective correct interpolation
// (c) www.scratchapixel.com
#include <cstdio>
#include <cstdlib>
#include <fstream>
typedef float Vec2[2];
typedef float Vec3[3];
typedef unsigned char Rgb[3];
inline
float edgeFunction(const Vec3 &a, const Vec3 &b, const Vec3 &c)
{ return (c[0] - a[0]) * (b[1] - a[1]) - (c[1] - a[1]) * (b[0] - a[0]); }
int main(int argc, char **argv)
{
Vec3 v2 = { -48, -10, 82};
Vec3 v1 = { 29, -15, 44};
Vec3 v0 = { 13, 34, 114};
Vec3 c2 = {1, 0, 0};
Vec3 c1 = {0, 1, 0};
Vec3 c0 = {0, 0, 1};
const uint32_t w = 512;
const uint32_t h = 512;
// project triangle onto the screen
v0[0] /= v0[2], v0[1] /= v0[2];
v1[0] /= v1[2], v1[1] /= v1[2];
v2[0] /= v2[2], v2[1] /= v2[2];
// convert from screen space to NDC then raster (in one go)
v0[0] = (1 + v0[0]) * 0.5 * w, v0[1] = (1 + v0[1]) * 0.5 * h;
v1[0] = (1 + v1[0]) * 0.5 * w, v1[1] = (1 + v1[1]) * 0.5 * h;
v2[0] = (1 + v2[0]) * 0.5 * w, v2[1] = (1 + v2[1]) * 0.5 * h;
#ifdef PERSP_CORRECT
// divide vertex-attribute by the vertex z-coordinate
c0[0] /= v0[2], c0[1] /= v0[2], c0[2] /= v0[2];
c1[0] /= v1[2], c1[1] /= v1[2], c1[2] /= v1[2];
c2[0] /= v2[2], c2[1] /= v2[2], c2[2] /= v2[2];
// pre-compute 1 over z
v0[2] = 1 / v0[2], v1[2] = 1 / v1[2], v2[2] = 1 / v2[2];
#endif
Rgb *framebuffer = new Rgb[w * h];
memset(framebuffer, 0x0, w * h * 3);
float area = edgeFunction(v0, v1, v2);
for (uint32_t j = 0; j < h; ++j) {
for (uint32_t i = 0; i < w; ++i) {
Vec3 p = {i + 0.5, h - j + 0.5, 0};
float w0 = edgeFunction(v1, v2, p);
float w1 = edgeFunction(v2, v0, p);
float w2 = edgeFunction(v0, v1, p);
if (w0 >= 0 && w1 >= 0 && w2 >= 0) {
w0 /= area;
w1 /= area;
w2 /= area;
float r = w0 * c0[0] + w1 * c1[0] + w2 * c2[0];
float g = w0 * c0[1] + w1 * c1[1] + w2 * c2[1];
float b = w0 * c0[2] + w1 * c1[2] + w2 * c2[2];
#ifdef PERSP_CORRECT
float z = 1 / (w0 * v0[2] + w1 * v1[2] + w2 * v2[2]);
// if we use perspective-correct interpolation we need to
// multiply the result of this interpolation by z, the depth
// of the point on the 3D triangle that the pixel overlaps.
r *= z, g *= z, b *= z;
#endif
framebuffer[j * w + i][0] = (unsigned char)(r * 255);
framebuffer[j * w + i][1] = (unsigned char)(g * 255);
framebuffer[j * w + i][2] = (unsigned char)(b * 255);
}
}
}
std::ofstream ofs;
ofs.open("./raster2d.ppm");
ofs << "P6\n" << w << " " << h << "\n255\n";
ofs.write((char*)framebuffer, w * h * 3);
ofs.close();
delete [] framebuffer;
return 0;
}计算样本深度需要使用顶点 z 坐标的倒数。 因此,我们可以在循环所有像素之前预先计算这些值(第 52 行)。 如果我们决定使用透视正确插值,则顶点属性值将除以与其关联的顶点的 z 坐标(第 48-50 行)。 下图左侧显示了未使用透视校正插值计算的图像,以及包含透视校正的插值图像(中)和 z 缓冲区内容的图像(作为灰度图像。对象距离屏幕越近,越亮):

尽管可以在左图中看到每种颜色似乎大致填充相同的区域,但差异很微妙。 这是因为在这种情况下,颜色是在 2D 三角形的“空间”内插值的(就好像三角形是与屏幕平面平行的平面一样)。 但是,如果你检查三角形顶点(和深度缓冲区),会注意到三角形根本不平行于屏幕(而是以一定角度定向)。 由于“绘制”为绿色的顶点比其他两个顶点更靠近相机,因此三角形的这一部分填充了屏幕的较大部分,这在中间图像中可见(绿色区域大于蓝色或红色区域) )。 中间的图像显示了正确的插值,以及使用 OpenGL 或 Direct3D 等图形 API 渲染此三角形时将得到的结果。
当应用于纹理时,正确和不正确的透视插值之间的差异更加明显。 在下一个示例中,我们将纹理坐标指定给三角形顶点作为顶点属性,并使用这些坐标为三角形创建棋盘图案。 使用或不使用透视正确插值渲染三角形作为练习。 在下图中你可以看到结果:

正如你所看到的,它还匹配具有在 Maya 中渲染的相同图案的相同三角形的图像。 希望我们的代码到目前为止似乎做了正确的事情。 与颜色一样,你需要做的就是(对于所有顶点属性都是如此)将纹理坐标(通常表示为 ST 坐标)除以它们关联的顶点的 z 坐标,然后在代码中,将纹理坐标插值值乘以 Z。以下是我们对代码所做的更改:
...
int main(int argc, char **argv)
{
Vec3 v2 = { -48, -10, 82};
Vec3 v1 = { 29, -15, 44};
Vec3 v0 = { 13, 34, 114};
...
Vec2 st2 = { 0, 0 };
Vec2 st1 = { 1, 0 };
Vec2 st0 = { 0, 1 };
...
#ifdef PERSP_CORRECT
// divide vertex-attribute by the vertex z-coordinate
c0[0] /= v0[2], c0[1] /= v0[2], c0[2] /= v0[2];
c1[0] /= v1[2], c1[1] /= v1[2], c1[2] /= v1[2];
c2[0] /= v2[2], c2[1] /= v2[2], c2[2] /= v2[2];
st0[0] /= v0[2], st0[1] /= v0[2];
st1[0] /= v1[2], st1[1] /= v1[2];
st2[0] /= v2[2], st2[1] /= v2[2];
// pre-compute 1 over z
v0[2] = 1 / v0[2], v1[2] = 1 / v1[2], v2[2] = 1 / v2[2];
#endif
...
for (uint32_t j = 0; j < h; ++j) {
for (uint32_t i = 0; i < w; ++i) {
...
if (w0 >= 0 && w1 >= 0 && w2 >= 0) {
...
float s = w0 * st0[0] + w1 * st1[0] + w2 * st2[0];
float t = w0 * st0[1] + w1 * st1[1] + w2 * st2[1];
#ifdef PERSP_CORRECT
float z = 1 / (w0 * v0[2] + w1 * v1[2] + w2 * v2[2]);
// if we use perspective correct interpolation we need to
// multiply the result of this interpolation by z, the depth
// of the point on the 3D triangle that the pixel overlaps.
s *= z, t *= z;
#endif
const int M = 10;
// checkerboard pattern
float p = (fmod(s * M, 1.0) > 0.5) ^ (fmod(t * M, 1.0) < 0.5);
framebuffer[j * w + i][0] = (unsigned char)(p * 255);
framebuffer[j * w + i][1] = (unsigned char)(p * 255);
framebuffer[j * w + i][2] = (unsigned char)(p * 255);
...
}
}
}
...
return 0;
}3、下一步是什么?
在本课的最后一章中,我们将简要讨论改进光栅化算法的方法(尽管我们不会具体实现这些技术)并解释本课的最终代码是如何工作的。
有原文链接:Perspective Correct Interpolation and Vertex Attributes
BimAnt翻译整理,转载请标明出处





