NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模
为了积分由于内散射而沿射线产生的入射光,我们将射线穿过的体块分解为小体块元素,并将每个小体块元素对整个体块对象的贡献结合起来,有点像我们在 2D 编辑软件(例如 Photoshop)中将带有遮罩或 Alpha 通道(通常代表对象的不透明度)的图像彼此堆叠在一起。 这就是我们在第一章中讨论 Alpha 合成方法的原因。 这些小体块元素中的每一个都代表第一章中提到的黎曼和中的一个样本。
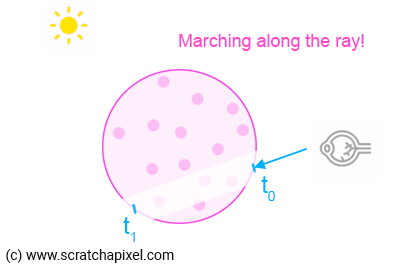
该算法的工作原理如下:
找到 t0 和 t1 的值,即相机/眼睛光线进入和离开体块对象的点。
将 t0-t1 定义的段分成 X 个相同大小的较小段。 一般来说,我们通过选择所谓的步长来实现这一点,步长只不过是定义较小线段长度的浮点数。 例如,如果 t0=2.5,t1=8.3,步长 = 0.25,我们将把 t0-t1 定义的段除以 (8.3-2.5)/0.25=23 个较小的段(现在让我们保持简单,所以不要担心小数)。
接下来要做的就是从 t0 或 t1 开始,沿着摄像机光线“行进”X 次(参见要点#6)。
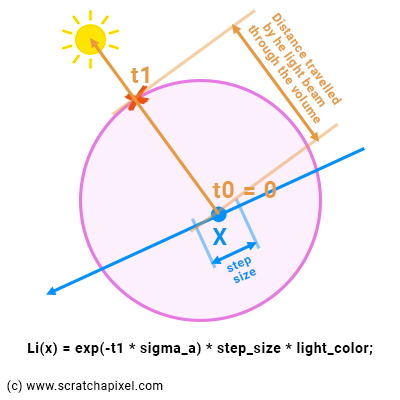
每次迈出一步,我们都会从步的中间(我们的样本点)向光源发射一条“光线”。 我们计算光线与体积元素相交(离开)的位置,并使用比尔定律计算其对样本的贡献(由于内散射)。 请记住,来自光源的光在穿过体块到达采样点时会被体块吸收。 这就是我们在上一章提到的黎曼和中的Li(x)值。 不要忘记,我们需要将此值乘以黎曼和中的步长,对应于 dx 项,即矩形的宽度。 在伪代码中我们得到:
// compute Li(x) for current sample x
float lgt_t0, lgt_t1; // parametric distance to the points where the light ray intersects the sphere
volumeSphere->intersect(x, lgt_dir, t0, lgt_t1); // compute the intersection of the light ray with the sphere
color Li_x = exp(-lgt_t1 * sigma_a) * light_color * step_size; // step_size is our dx
...如图 2 所示,射线与球体相交测试的 t0 应始终为 0,因为光线从球体内部开始,而 t1 是从样本位置 x 到光线与球体相交点的参数距离。 因此,我们可以使用比尔定律方程中的该值来计算体块物体吸收光的距离。
当然,穿过小体块元件(我们的样品)的光在穿过采样时也会衰减。 因此,我们使用步长作为比尔定律方程中光束穿过体块的距离值来计算样本的透射值。 然后将光量(内散射)衰减(乘以)该透射值。
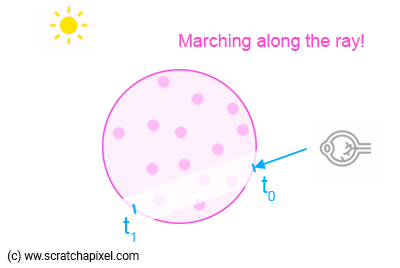
最后,我们需要组合每个样本,以说明它们各自对体块对象的整体不透明度和“颜色”的贡献。 事实上,如果向后思考这个过程(如图 1 所示),第一个体块元素(从 t1 开始)被第二个体块元素遮挡,第二个体块元素本身又被第三个体块元素遮挡,依此类推,直到我们到达“队列”中的最后一个元素(紧邻 t0 的样本)。 如果“通过相机”射线查看,紧邻 t1 的元素会被它前面的所有元素遮挡。 紧邻 t0 的样本之后的样本被第一个样本遮挡,依此类推。
“光线行进”这个名字现在很容易理解:我们沿着射线行进,采取小的规则步骤,如图 1 所示(向后光线行进的示例)。 请注意,使用常规步骤并不是光线行进算法的条件。 步数也可以是不规则的,但为了让事情简单起见,让我们使用常规步数或跨步(肯·马斯格雷夫喜欢这样称呼它们)。 当使用常规步骤时,我们称之为统一光线处理(而不是自适应光线行进)。
我们可以通过两种方式组合样本:向后(从 t1 行进到 t0)或向前(从 t0 行进到 t1)。 一个比另一个更好(某种程度上)。 我们现在将描述它们是如何工作的。
1、后向射线行进
在向后射线行进中,我们将沿着射线从后向前行进。 换句话说,从 t1 到 t0。 这改变了我们组合样本来计算最终像素不透明度和颜色值的方式。
很自然,因为我们从体块对象(我们的球体)的背面开始,所以我们可以用背景颜色(我们的蓝色)初始化像素颜色(为相机光线返回的颜色)。 但在我们的实现中,我们只会在过程结束时将两者结合起来(一旦我们计算了体块对象颜色和不透明度),有点像我们在 2D 编辑软件中合成两个图像时。
我们将计算第一个样本(例如 X0)在体积中的贡献,从 t1 开始,然后回到 t0,采取常规步骤(由步长定义)。
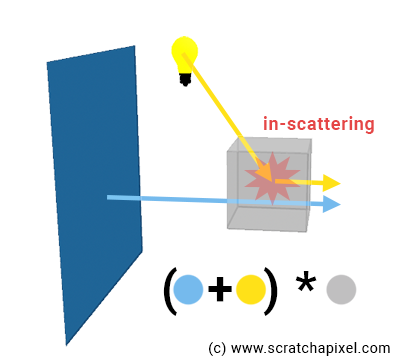
该样本的贡献是什么?
我们将计算内散射贡献(光源的贡献)Li(X0),如上所述(第 6 点):沿光的方向发射光线,然后使用比尔定律衰减光贡献,以计算当光从进入物体的点(我们的球体)传播到采样点 (X0) 时,有多少光被体块物体吸收。
然后,我们需要将该光乘以采样的透明度值(表示样品吸收了多少光)。 再次使用比尔定律计算采样透明度,使用步长作为光束穿过该采样的距离(图 3)。
...
color Li_x0 = exp(-lgt_t1 * sigma_a) * light_color * step_size; // step_size is our dx
color x0_contrib = Li_x0 * exp(-step_size * sigma_a);
...我们刚刚计算了第一个样本 X0。 然后我们转向第二个样本 (X1),但现在我们需要考虑两个光源:来自第一个样本 X0 的光束(我们之前的结果),以及由于内散射而穿过第二个样本的光束 X1\。 我们已经计算了前者(正如我们刚才所说,这是我们之前的结果)并且我们知道如何渲染后者。 我们将它们相加,并将该总和乘以第二个样本传输值。 这成为我们的新结果。 我们不断地用 X2、X3 重复这个过程,直到我们最终到达 t0\。 最终结果是体块对象对当前相机光线像素颜色的贡献。 这个过程如下图所示。
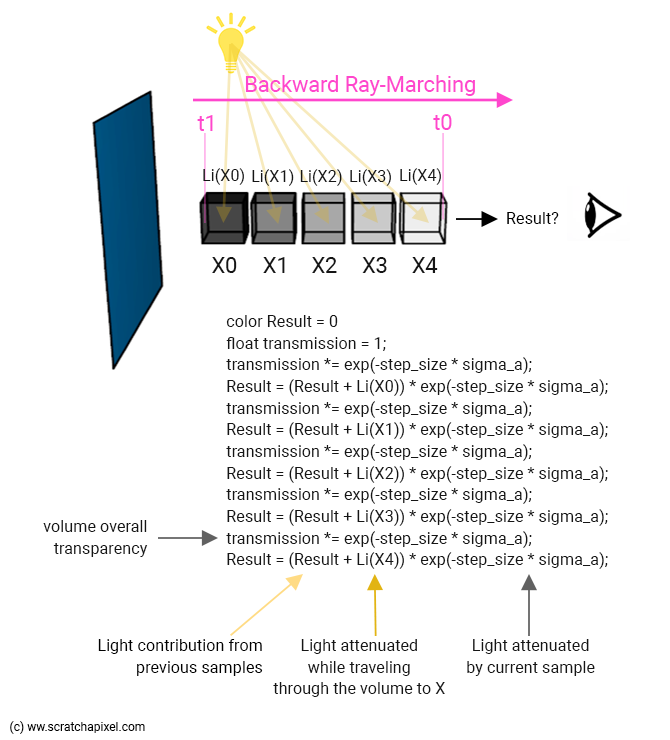
从上图中请注意,我们计算两个值:体块整体颜色(存储在结果中)和整体透明度。 我们将此值初始化为 1(完全透明),然后当我们沿着光线向上(或向下)移动(从 t1 到 t0)时,使用每个样本透明度值来衰减该值。 然后(最终)我们可以使用这个整体透明度值将体块对象与背景颜色结合起来。 简单计算如下:
color final = background_color * transmission + result;在合成术语中,我们会说“结果”项已经预先乘以体块整体透明度。 但如果这让你感到困惑,我们将在下一章中澄清这一点。 所以现在不要太关注这个。
另请注意,在上图中和下面的代码中,样本的衰减项始终相同:exp(-step_size * sigma_a)。 当然,这效率不高。 你应该计算该项一次,将其存储在变量中,然后使用该变量。 但清晰是我们的目标,而不是编写高性能代码。 此外,目前,当我们沿着射线行进时,该值是恒定的,但我们将在接下来的章节中发现它最终会因样本而异。
翻译成代码是这样的:
constexpr vec3 background_color{ 0.572f, 0.772f, 0.921f };
vec3 integrate(const vec3& ray_orig, const vec3& ray_dir, ...)
{
const Object* hit_object = nullptr;
IsectData isect;
for (const auto& object : objects) {
IsectData isect_object;
if (object->intersect(ray_orig, ray_dir, isectObject)) {
hit_object = object.get();
isect = isect_object;
}
}
if (!hit_object)
return background_color;
float step_size = 0.2;
float sigma_a = 0.1; // absorption coefficient
int ns = std::ceil((isect.t1 - isect.t0) / step_size);
step_size = (isect.t1 - isect.t0) / ns;
vec3 light_dir{ 0, 1, 0 };
vec3 light_color{ 1.3, 0.3, 0.9 };
float transparency = 1; // initialize transparency to 1
vec3 result{ 0 }; // initialize the volume color to 0
for (int n = 0; n < ns; ++n) {
float t = isect.t1 - step_size * (n + 0.5);
vec3 sample_pos= ray_orig + t * ray_dir; // sample position (middle of the step)
// compute sample transparency using Beer's law
float sample_transparency = exp(-step_size * sigma_a);
// attenuate global transparency by sample transparency
transparency *= sample_transparency;
// In-scattering. Find the distance traveled by light through
// the volume to our sample point. Then apply Beer's law.
IsectData isect_vol;
if (hitObject->intersect(sample_pos, light_dir, isect_vol) && isect_vol.inside) {
float light_attenuation = exp(-isect_vol.t1 * sigma_a);
result += light_color * light_attenuation * step_size;
}
// finally attenuate the result by sample transparency
result *= sample_transparency;
}
// combine with background color and return
return background_color* transparency + result;
}但请注意这段代码。 目前还不准确。 它缺少一些我们将在下一章中讨论的术语。 现在,我们只想让你了解光线行进的原理。 然而这段代码将产生一个令人信服的图像。

请注意,在本例中,我们使用了自上而下的远距离光(光方向沿 y 轴向上)。 球体的微红色来自于浅色。 你可以看到球体的上半部分比下半部分更亮。 阴影效果已经可见。
让我们再次看看当我们沿着射线行进时样本会发生什么:

当我们完成循环时,如果你看看Li(X0)发生了什么,可以观察到它乘以样本衰减的某个幂。 我们沿着光线行进的次数越多,指数就越高(首先是 1,然后是 2,然后是 3,...),因此结果越小(因为衰减或样本透明度低于 1)。 换句话说,随着更多样本的积累,第一个样本对整个体积散射光的贡献会减少。
2、前进射线行进
在计算 Li(x) 和样本的透射值时,后向射线行进没有区别。 不同的是我们如何组合样本,因为这一次,我们将从 t0 行进到 t1(从前到后)。 在前向射线行进中,样本散射光的贡献必须通过我们迄今为止处理的所有样本(包括当前样本)的总体透射(透明度)值来衰减:Li(X1) 通过样本 X0 和 X1 的透射值衰减,Li(X2) 通过样本 X0、X1 和 X2 的透射值遮挡,等等。以下是算法的说明:
步骤1:在进入射线行进循环之前:将整体透射(透明度)值初始化为1,将结果颜色变量初始化为0(存储当前相机光线的体积对象颜色的变量):float Transmission = 1; 颜色结果 = 0;。
步骤 2:对于光线行进循环中的每次迭代:
计算当前样本的内散射:Li(x)。
通过将其乘以当前样本透射值来更新总体透射(透明度)值:
transmission*=sample_transmission。将 Li(x) 乘以总透射(透明度)值:样本散射的光被我们迄今为止处理的所有样本(包括当前样本)遮挡。 将结果添加到存储当前相机光线体积颜色的全局变量中:
result += Li(x) * transmission.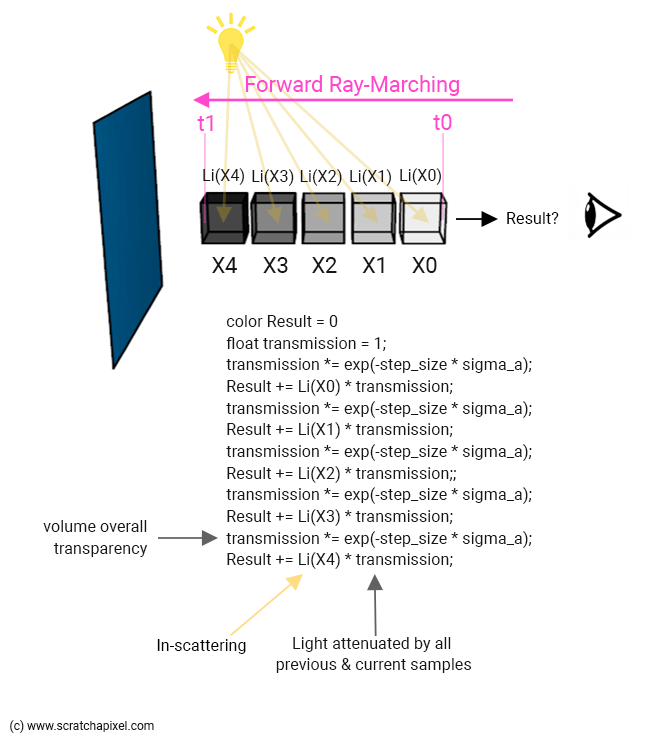
翻译成代码:
...
vec3 integrate(const vec3& ray_orig, const vec3& ray_dir, ...)
{
...
float transparency = 1; // initialize transparency to 1
vec3 result{ 0 }; // initialize the volume color to 0
for (int n = 0; n < ns; ++n) {
float t = isect.t0 + step_size * (n + 0.5);
vec3 sample_pos = ray_orig + t * ray_dir;
// current sample transparency
float sample_attenuation = exp(-step_size * sigma_a);
// attenuate volume object transparency by current sample transmission value
transparency *= sample_attenuation;
// In-Scattering. Find the distance traveled by light through
// the volume to our sample point. Then apply Beer's law.
if (hit_object->intersect(sample_pos, light_dir, isect_vol) && isect_vol.inside) {
float light_attenuation = exp(-isect_vol.t1 * sigma_a);
// attenuate in-scattering contrib. by the transmission of all samples accumulated so far
result += transparency * light_color * light_attenuation * step_size;
}
}
// combine background color and volumetric object color
return background_color * transparency + result;
}但请注意这段代码。 目前还不准确。 它缺少一些我们将在下一章中讨论的术语。 现在,我们只想让你了解光线行进的原理。 然而这段代码将产生一个令人信服的图像。
无需在此处显示图像。 如果我们做得正确,向后和向前的射线行进应该给出相同的结果。 好吧,我们知道您不会认为这是理所当然的,所以这是结果。

3、为什么前向射线行进比向后射线行进“更好”?
因为一旦体积的透明度非常接近 0,我们就可以停止光线行进(如果体积足够大和/或散射系数足够高,就会发生这种情况)。 只有当你以光线行进的方式前进时,这才有可能实现。
现在,渲染我们的球体相当快,但随着我们继续阅读章节,你会发现它最终会变慢。 因此,如果我们能够避免计算对像素颜色没有贡献的样本,因为我们沿着光线行进时到达了一个点,我们知道体块是不透明的,那么这是一个很好的优化。
我们将在下一章中实现这个想法。
4、选择步长
请记住,我们进行射线行进,从 t0 到 t1 采取小步长的原因是使用黎曼求和方法来估计积分(由于内散射而沿着相机光线向眼睛散射的光量)。 正如前一章和阴影数学课程中所解释的,用于估计积分的矩形越大(在我们的例子中,矩形的宽度由此处的步长大小定义),近似值就越不准确。 或者反过来:矩形越小(步长越小),估计就越准确,但计算时间当然也就越长。 目前,渲染球体的速度相当快,但随着我们学习本课程,您会发现它最终会变得慢得多。 这就是为什么选择步长是速度和准确性之间的权衡。
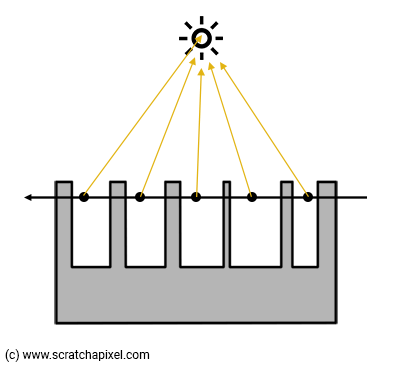
现在,我们假设体积密度也是均匀的。 在接下来的章节中,我们将看到为了渲染云或烟雾等体积密度,密度会随着空间的变化而变化。 这些体积由大频率特征和较小频率特征组成。 如果步长太大,最终可能无法捕获一些较小的频率特征(图 5)。 这是一个过滤问题,本身就是一个重要但复杂的主题。
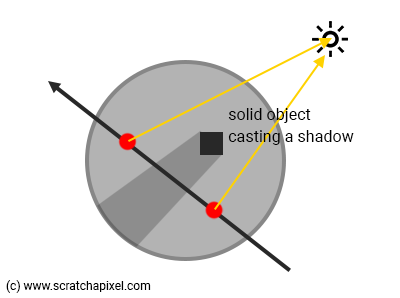
可能会出现另一个需要调整步长的问题:阴影。 如果小固体对象在体积对象上投射阴影,如果步长太大,最终将错过它们(图 6)。
所有这些并没有告诉我们如何选择一个好的步长。 理论上来说,没有任何规则。 你基本上应该了解体积对象的大小。 例如,如果它是一个矩形,充满了某种均匀气氛的房间,你应该了解该房间的大小(以及使用的单位类型,例如 1 单位 = 10 厘米)。 因此,如果房间有 100 个单位大,则 0.1 的步长可能太小,而 1 或 2 可能是一个不错的起点。 然后,你需要像我们之前提到的那样,在速度和准确性之间找到一个良好的权衡。
现在看来,这也不完全正确。 在通过考虑场景中物体的大小来凭经验选择步长时,必须有一种更合理的方法来这样做。 一种可能的方法是考虑进入体积对象的距离处的像素“有多大”,并将步长设置为投影像素的尺寸。 事实上,作为离散对象的像素无法表示场景中小于其大小的细节。 我们不会在这里讨论更多细节,因为过滤本身就值得一课。 现在我们要说的是,一个好的步长接近于相机光线与体积相交点处的像素的投影大小。 这可以通过以下方式进行估计:
float projPixWidth = 2 * tanf(M_PI / 180 * fov / (2 * imageWidth)) * tmin;如果你愿意,可以对其进行优化。 其中 tmin 是相机光线与体积对象相交的距离。 我们可以类似地计算光线离开体积的投影像素宽度,并在 tmin 和 tmax 处对投影像素宽度进行线性插值,以设置我们沿着射线行进时的步长。
5、其他感兴趣的考虑因素!
编写生产代码需要将光线不透明度和颜色与光线数据一起存储。 这样我们就可以首先对固体对象进行光线追踪,然后对体块对象进行光线追踪,并结合结果(与上例中将背景颜色与体积球体对象相结合的方式类似)。
请注意,相机光线的路径上可以有多个体块对象。 因此,有必要沿途存储不透明度,并在我们对连续体块对象进行光线行进时组合它们的不透明度和颜色。
体块对象可以由组合对象的集合组成,例如彼此重叠的立方体或球体。 在这种情况下,我们可能希望将它们组合成某种聚合结构。 对此类聚合进行光线行进需要特别小心地计算生成聚合的对象的相交边界。
原文链接:The Ray-Marching Algorithm
BimAnt翻译整理,转载请标明出处





