Z-Fighting 权威指南

NSDT工具推荐： Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模

Z-Fighting 是渲染管道中深度测试中出现的问题。它是由深度值的有限数值精度引起的。故障将表现为不正确的渲染，即屏幕上错误地显示应该被遮挡在另一个后面的对象。故障主要发生在透视投影变换中，但也可能发生在正交投影变换中。到目前为止，一个众所周知的好的解决方案是使用对数深度测试，但在实施和使用它时必须小心谨慎。无论哪种方式，要处理 Z-Fighting，重要的是正确识别给定条件下的定量限制。

这篇博文旨在成为处理 Z-Fighting 的实用信息来源。它通过简短的理论分析说明了它发生的原因和方式，然后展示了一些使用 OpenGL 实际实现的数值结果。然后，它讨论了有关对数深度测试的一些实现问题。它还附带了三个与 OpenGL 配套的工具。利用这些工具，你可以直观地看到 Z-Fighting 的效果，并通过设置适合你环境的参数来进行实验。

1、关键要点

这篇博文有三个要点，对建模者和开发人员设计 3D 模型和场景以及开发渲染系统很有用。如果你还不熟悉坐标变换和深度测试，可以跳过本节。

1.1 一般规则

在对这个主题进行了一些研究并进行了一些分析和实验后，我推荐以下一般规则。

• 在适用的情况下，在片段着色器中使用 NF 类型的对数深度和 gl_FragDepth。
• 如果片段着色器的 GPU 工作负载成为问题，并且你想要启用早期片段测试，您有两种选择：一种是将对数深度设置为 gl_Position.z，以牺牲扭曲的几何形状为代价。另一种是回到普通的透视投影深度，增加远处物体的 Z 竞争。你可能必须按从后到前的顺序在多个绘制调用中渲染场景，每个绘制调用都使用清除的深度缓冲区。

1.2 避免 Z-Fighting 的最小间隙

本篇博文的共同主题是以下问题：

假设有两个点彼此靠近，在 VCS 中与相机的距离约为 z。视线方向上这两个点之间需要多少间隙 Δz，才能在 SCS 中正确比较它们的深度？

VCS 和 SCS 分别表示视图坐标系和屏幕坐标系。它们将在下文中解释。

首先得出结论，以下是本篇博文中最重要的两个图表。

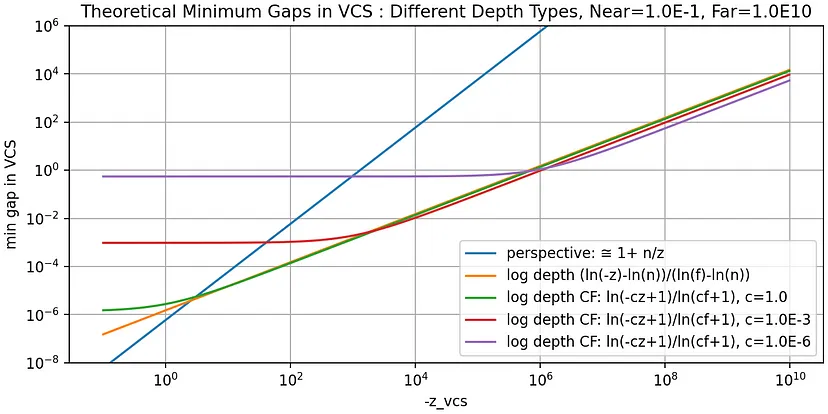
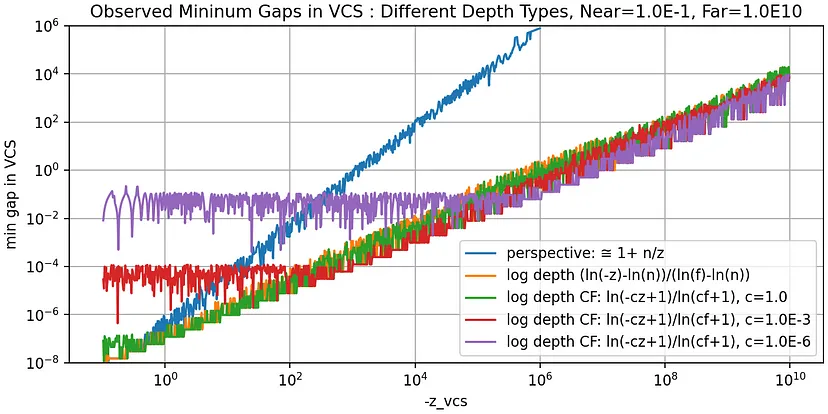
上面的第一张图表显示了假设深度格式为 OpenGL 中的 GL_DEPTH24_STENCIL8 的理论值。第二张图表显示了从测试程序中获取的采样值，稍后将对其进行描述。每条线或图下方的区域是发生错误比较或 Z-Fighting 的地方。例如，如果两个物体距离相机 10² = 100 [m]，如果使用 C=1/10⁶ 的 CF 类型对数深度，则这两个物体在视线上的距离必须至少为 0.1–0.6 [m]。透视（普通）深度类型的最小距离约为 0.01 [m]，其他深度类型的最小距离约为 100 [μm]。

1.3 在顶点着色器中将对数深度分配给 gl_Position 的效果

一些实现通过启用早期片段测试将对数深度分配给 gl_Position 以减少片段着色器的调用。然而，它带来了由视锥剔除和光栅化中的线性插值引起的负面影响。这种负面影响扭曲了几何形状。由于很难通过图表显示效果，本博文附带了一个交互式工具，可以实时直观地查看效果。以下是使用 OpenGL 实现的工具的屏幕截图。

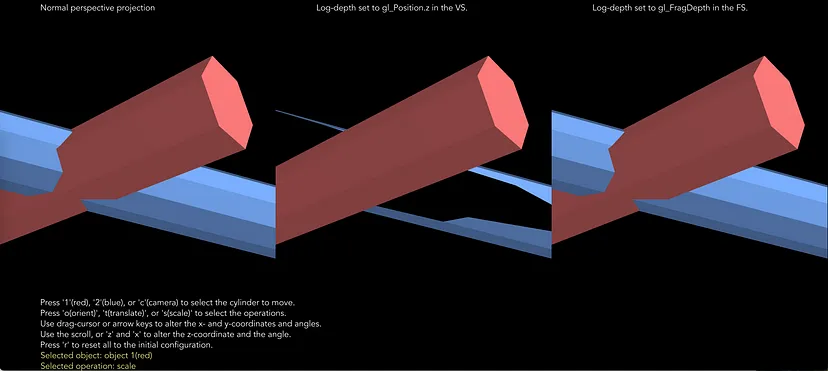
左窗格由普通透视投影渲染，没有对数深度测试。右窗格使用片段着色器中设置为 gl_FragDepth 的对数深度进行渲染。中间窗格使用对数深度 gl_Position.z 进行渲染，这会扭曲几何图形，如图所示，遮挡不正确，多边形形状扭曲。

以上就是我在开头想要分享的三个关键点。

2、坐标变换回顾

本节简要介绍图形管道中从 3D 世界坐标系到 2D 屏幕坐标系的变换。它假设 OpenGL 和 GLFW 处于渲染管道的最后阶段，但它也适用于其他技术，例如 Vulkan 和 Metal。

2.1 相机方向

按照惯例，相机在其局部坐标系 (LCS) 中的方向是朝向负 Z 方向，垂直向上方向与正 Y 方向对齐。如后所述，它与视图坐标系相同。

2.2 在 WCS 中放置和定位相机

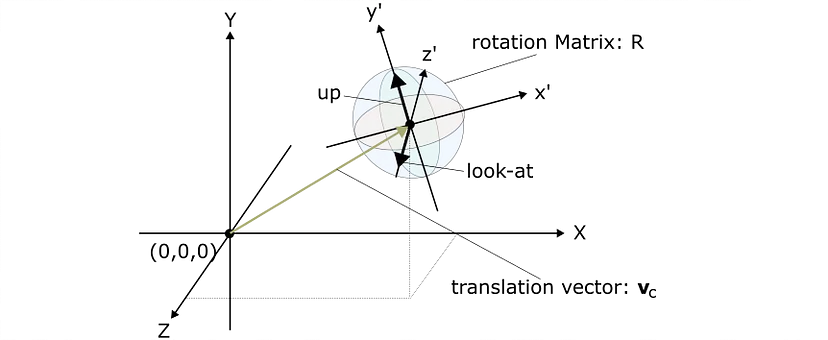
相机通过旋转矩阵 R 和平移向量 v_c 放置在世界坐标系或 WCS 中。它们组合成 4x4 模型矩阵，如下所示：

2.3 将世界带入相机的 LCS

要通过相机（也是在 WCS 中放置和定向）查看在 WCS 中放置和定向的物体，你需要将这些物体带入相机的局部坐标系。这是由视图矩阵定义的视图变换，它是相机模型矩阵的逆。结果坐标系是视图坐标系或 VCS。这与相机的 LCS 相同。

2.4 从 VCS 到 NDCS，再到 SCS

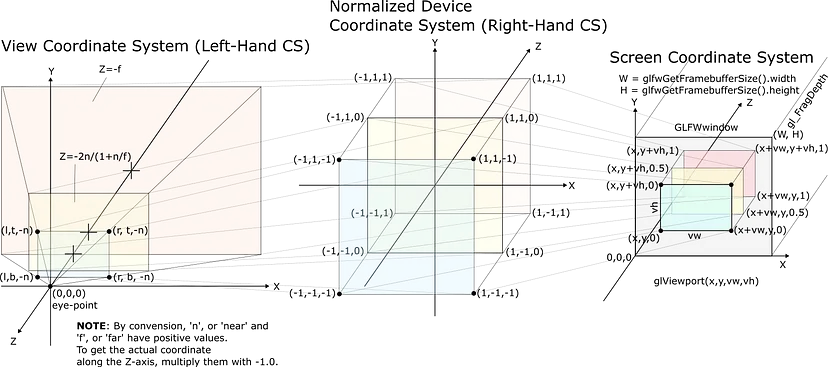
VCS 中的坐标被变换到标准化设备坐标系，即 NDCS。在 VCS 的负 Z 区域中定义的视锥体被变换为以 NDCS 中的原点为中心的立方体。VCS 的正 Z 区域（视点后面）被变换为 NDCS 中平面 z=f/(f-n) 后面的区域。在 NDCS 中，VCS 中平面 z=0 的变换未定义。

NDCS 中的坐标最终被变换为屏幕坐标系，即 SCS，其中使用 Z 缓冲区执行深度测试。对于 OpenGL（假设 GL_DEPTH24_STENCIL8），Z 轴上的值范围从 VCS 中的 [-far, -near) 变为 NDCS 中的 [-1.0, 1.0)，然后变为 SCS 中的 [0, (2²⁴-1)/2²⁴]。请注意，SCS 是 x 和 y 方向的光栅化整数坐标空间，以及 z 方向的步长为 1/2²⁴ 的定点数空间：

透视矩阵的定义也如上所示。请注意，Z 轴的方向通过透视变换翻转。VCS 是左手坐标系，而 NDCS 是右手坐标系。如果我们关注 Z 轴，则从 VCS 到 NDCS 的变换如下：

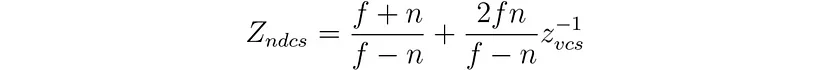
对于 OpenGL，SCS 中的 Z 坐标是通过 NDCS 中的 Z 坐标获得的，并进行以下简单的转换：

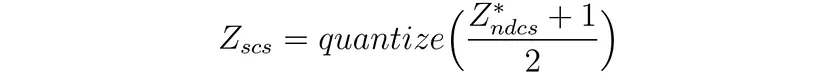
Z*_ndcs 是 Z_ndcs 的采样和插值。深度测试在 SCS 中使用 Z 缓冲区进行。由于量化，如果 |z_1 - z_2| ≤ 1/2²³，则 NDCS 中的两个不同 Z 坐标 z_1 和 z_2 可以在 SCS 中获得相同的值，从而导致 Z-fighting。

3、使用透视投影进行深度分析

如果我们忽略插值和量化的影响，则 Z 坐标从 VCS 到 SCS 的映射由以下函数给出：

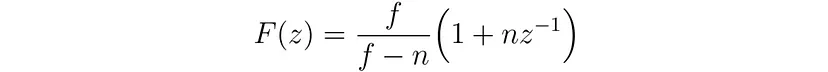
导数为：

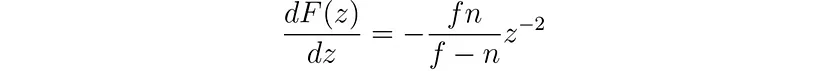
假设导数在 z 附近不变，并且考虑到 Z 缓冲区的粒度为 1/2²⁴，则 VCS 中 Z 坐标所需的最小间隙  Δz_vcs 如下所示：

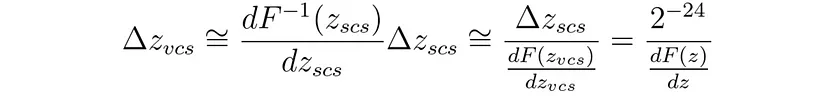
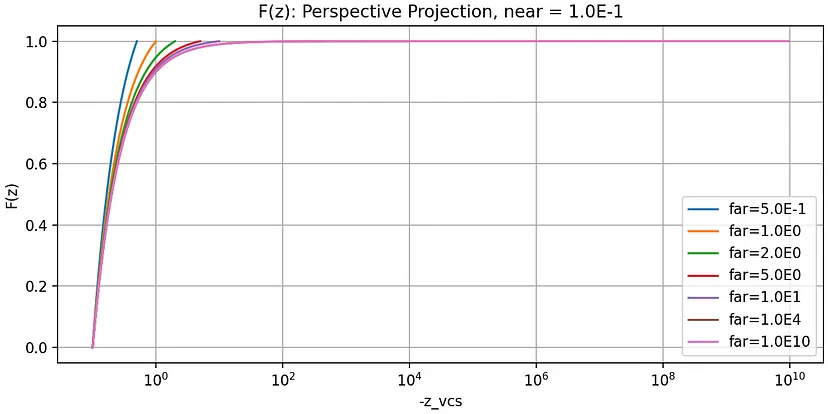
下图显示了 n = 0.1 和 f 在不同位置的这些函数图。0.1 处的近平面可以解释为距离眼睛 0.1 [m] 的取景器：

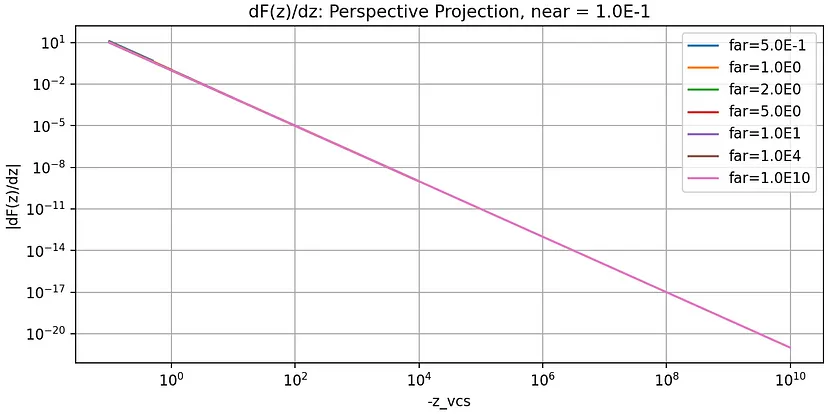
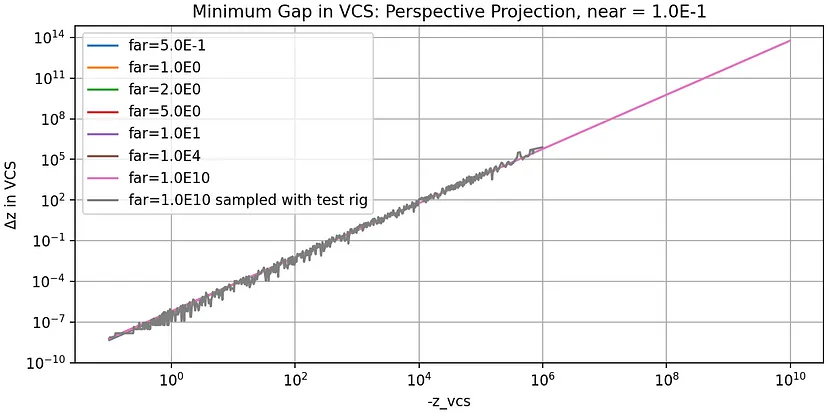
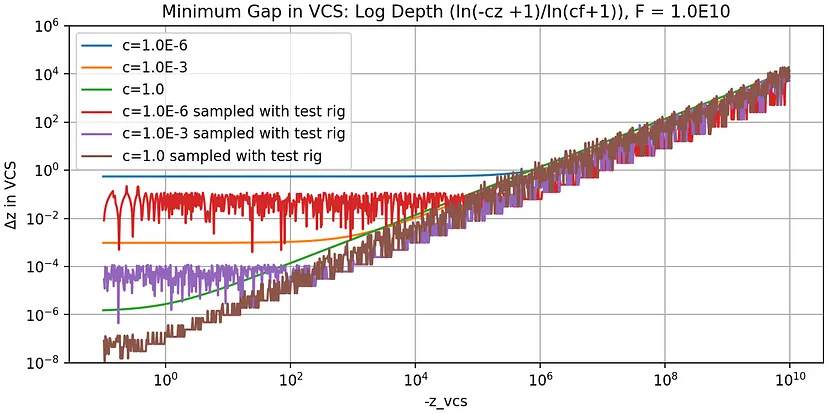
最后一张图表还显示了使用 OpenGL 实现的批处理测试程序观察到的最小间隙图。它是三个附带工具之一，稍后将在下面描述。

分析

正如最后一张图表所示，所需的最小间隙逐渐增加，深度测试在大约 -z_vcs > near * 1.0E6 时几乎无用。如果两个物体距离相机 1 [km]，最小间隙将约为 1 [m]。

此外，一些文章建议将近平面和远平面放置得尽可能近，以充分利用 SCS 中的 [0,1.0] 范围，但正如第二张和第三张图表所示，它对最小间隙几乎没有影响，除非视锥体变得像煎饼一样非常浅，但在这种情况下，使用透视投影就没有什么意义了。

4、对数深度的分析：NF 类型

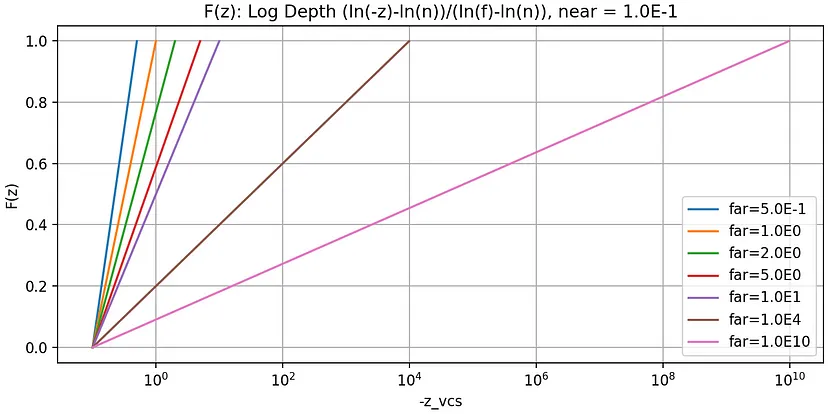
透视投影中的深度值的问题在于它很快趋近于 1.0 并保持相对平坦，即 dF(z)/dz 很快趋近于 0。希望找到一个从 VCS 到 SCS 的映射函数 F(z)，其导数 dF(z)/dz 保持相对较高。此外，它必须具有以下特征。

• F(-near) ≥ 0 且 F(-far) ≤ 1。
• F(z) 是一对一映射。
• F(z) 单调递减，即 -z1_vcs > -z2_vcs => z1_scs > z2_scs。

下面的对数深度就是这样一个函数：

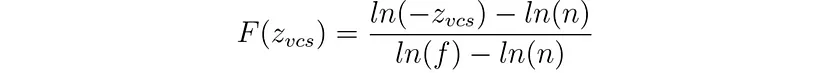
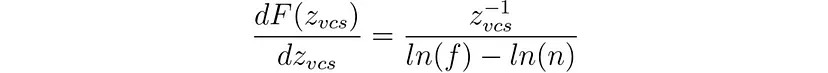
以下3张图表分别显示了函数图、理论最小间隙和测试程序中的观测值：

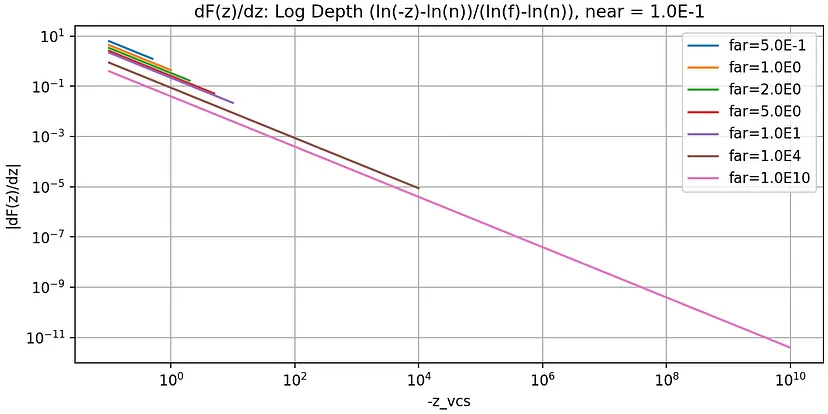
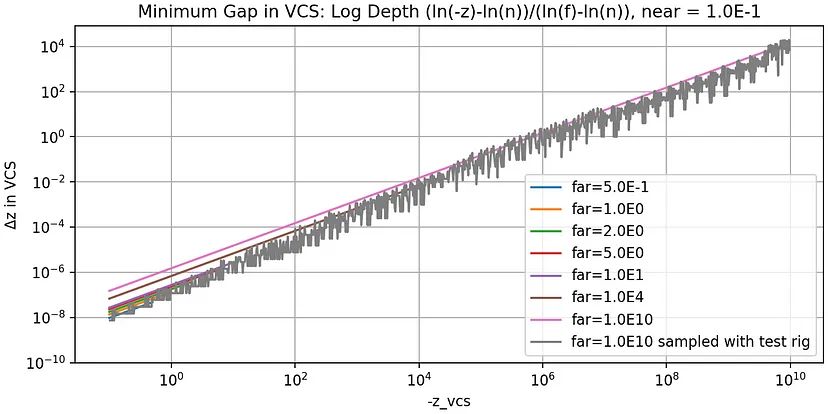
分析

如第三张图所示，与使用普通透视投影进行映射相比，对数深度的最小间隙更为有利。

对于距离相机约 1 [km] 的两个物体，最小间隙将为 1 [mm]（火腿片）。对于距离相机 1 [m] 的两个物体，最小间隙将为 1 [μm]（细菌大小）。无论距离（近、远），距离与间隙的比率都保持不变，为 1/10⁶。

5、对数深度的分析：CF 类型

这是对数深度映射的参数形式，参数为“c”[Outerra2009]。这似乎是试图进一步改进 NF 类型，将伪近平面拉近到远平面，而不缩小 F(z) 的范围。参数“c”可以被认为是“近”的倒数，即 c=1/n。定义及其导数如下：

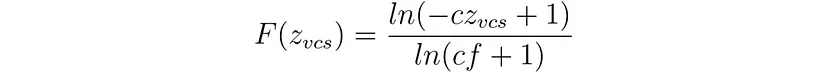
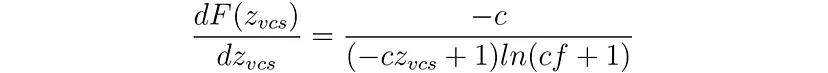
下图显示了 f = 10¹⁰ 和 c = 1.0、1/10³ 和 1/10⁶ 的图：

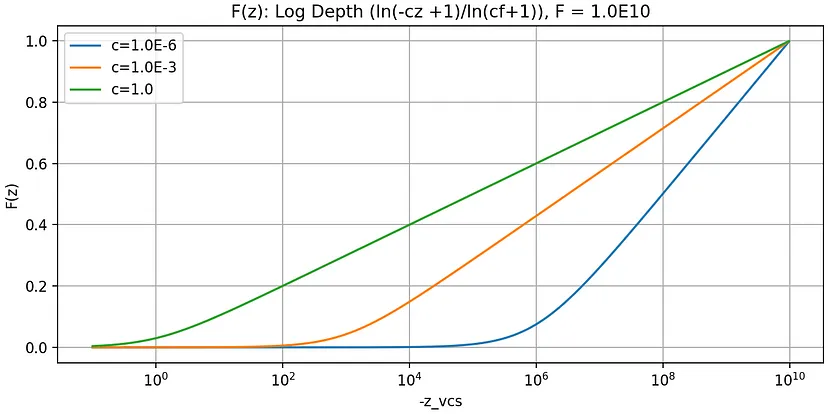
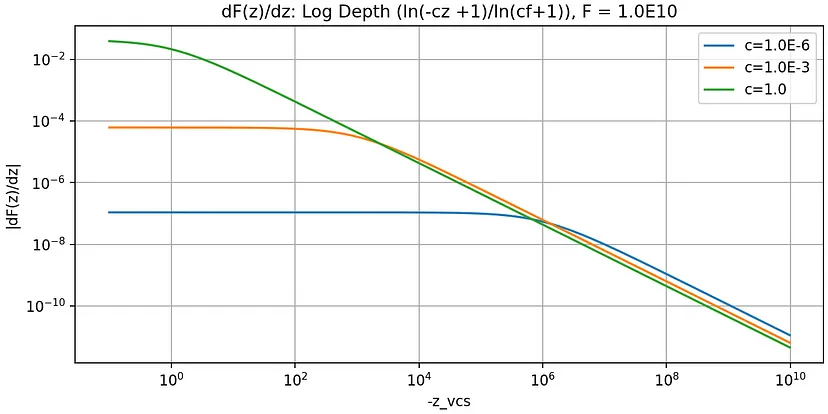
分析

与 NF 类型相比，使用 CF 类型的增益很小。

可以使用以下近似导数分析 NF 和 CF 类型之间的差异。

对于 NF 类型：

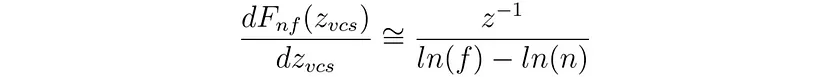
对于CF类型：

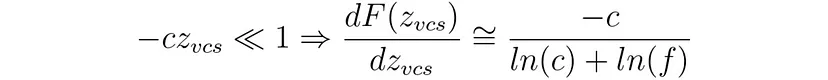
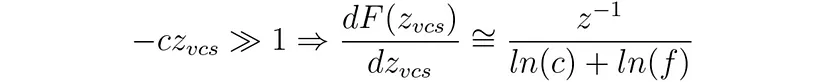
如果 -z_vcs 足够大，主要区别在于分母。如果我们设置 c=1/n，这两种类型大致相同。如果我们设置 n=1/10¹ 和 c=1/10⁶，那么：

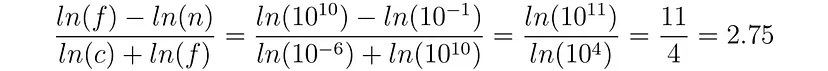
粗略地说，CF 类型所需的最小间隙将比 NF 类型的间隙小 2.75 倍。如果 c=1/10³，则为 11/7 =1.57 如果 c=1.0，则增益为 11/10=1.1。

如果 -z_vcs 较小，则 dF(z)/dz 和 CF 类型的最小间隙将变为常数。如果 c=1/10⁶，则 |dF(z)/dz| ≅1.09/10⁷，最小间隙 ≅ 0.55 [m]。如果 c=1/10³，则 |dF(z)/dz| ≅ 6.0/10⁵，最小间隙 ≅ 9.6/10⁴ ≅ 1 [mm]

如上所示，与 NF 类型相比，你必须将 c 设置为明显较低的值，例如 c = 1/10⁶，这样 -z_vcs * c >> 1.0 才能获得一些有意义的增益，但缺点是 -z_vcs * c << 1.0 的最小间隙较大。

对于大多数实际用例， c = 1/10⁶ 是不切实际的，因为对于较小的 Z 坐标，最小间隙较大。如果 c = 1/10³，则对于许多用例而言都是可以接受的，但对于较大的 Z 坐标而言，你获得的增益并不大。

上述论点意味着 NF 类型将适用于大多数用例。深度测试的分析到此结束。让我们继续讨论实施问题。

6、对数深度着色器的实现

本部分给出几种着色器的实现。

6.1 使用 gl_FragDepth 的 NF 类型的示例实现

以下是示例顶点着色器，它将 VCS 的 Z 坐标传递到变量 position_vcs_z 中的片段着色器上：

#version 330 core

in vec4 position_lcs;

uniform mat4 P;
uniform mat4 V;
uniform mat4 M;

out float position_vcs_z;

void main() {

    position_wcs = M * position_lcs;
    vec4 position_vcs = V * position_wcs;
    position_vcs_z = position_vcs.z;
    gl_Position  = P * position_vcs;
}

下面是一个示例片段着色器，它使用 position_vcs_z 中 VCS 中的（插值）Z 坐标设置 NF 类型的对数深度。它将深度值设置为 gl_FragDepth：

#version 330 core

in float position_vcs_z;

uniform float log_far;  // = log( 1.0e6  );
uniform float log_near; // = log( 1.0e-1 );

out vec4 color_out;

void main()
{

    float log_z = log( max( 1.0e-30, -1.0 * position_vcs_z ) );
    gl_FragDepth = ( log_z - log_near ) / ( log_far - log_near );

    color_out = vec4( 1.0, 1.0, 1.0, 1.0 );
}

问题：无法应用早期深度测试。

由于在片段着色器中明确为 gl_FragDepth 分配了一个值，因此无法启用早期片段测试。即使使用 GL_ARB_conservative_depth 也是如此，如下所示。

如果启用了 GL_ARB_conservative_depth，你可以重新声明 gl_FragDepth，如下所示：

#extension GL_ARB_conservative_depth : enable
layout(depth_less) out float gl_FragDepth;

属性必须是 depth_less，因为对于域 -far < z < -near， |F(z)| < |gl_Position.z/gl_Position.w|。它不会启用早期深度测试，因为片段着色器可以将像素向前移动，使其在 SCS 中具有较小的 Z 坐标。要在片段着色器中通过显式分配 gl_FragDepth 来启用早期深度测试，属性应该是 depth_greater，假设指定了普通的 glDepthFunc(GL_LESS)。

6.2 使用 gl_Position.z 实现 NF 类型的示例

以下代码片段是一个示例顶点着色器，它将对数深度分配给 gl_Position.z。请注意，分配给 gl_Position 的深度值不是在范围为 [0,1) 的 SCS 中，而是在范围为 [-1, 1) 的 NDCS 中。

片段着色器没有任务，因为深度隐式设置为 2.0 * gl_FragCoord.z/gl_FragCoord.w - 1：

#version 330 core

in vec4 position_lcs;
uniform mat4 P;
uniform mat4 V;
uniform mat4 M;
uniform float log_far;  // = log( 1.0e6  );
uniform float log_near; // = log( 1.0e-1 );

void main() {
    position_wcs = M * position_lcs;
    vec4 position_vcs = V * position_wcs;
    gl_Position  = P * position_vcs;
    float log_z_vcs = log( max( 1.0e-30, -1.0 * position_vcs.z ) );
    float log_z_ndcs = (log_z_vcs - log_near)/(log_far - log_near) * 2.0 - 1.0;
    gl_Position.z = log_z_ndcs * gl_Position.w;
}

问题：几何失真

在 gl_Position 中分配深度可启用早期片段测试，因此可以通过减少片段着色器的调用次数来减少 GPU 工作量。但是，由于管道中片段着色器之前的采样器和光栅化器的插值取决于 gl_Position 中的值，因此更改其中的 Z 坐标会扭曲几何图形。特别是，如果顶点位于相机后面，即 VCS 中的 Z 坐标为正，则必须将它们限制为某些负值。失真的严重程度很难定量分析，但这里有一个基于一些实验的经验法则。

• 要渲染的对象的顶点应位于视锥体中。越靠近中心，失真越少。

例如，如果你渲染由靠近屏幕中心的一些细网格组成的 3D 对象，它将相当无失真。但是，你应该避免以下类型的对象：

• 横跨视锥体或横跨正 Z 区域和负 Z 区域的地板砖。
• 由长三角形组成或到达视锥体两侧的长梁。
• 由细长条带组成的网格图案。

一般来说，你应该避免在顶点着色器中分配深度。如果你确实必须使用这种类型，必须始终注意几何图形会被扭曲。

7、工具

本文附带了三种工具。它们位于 Github 存储库中。

7.1 depth_test_interactive

此工具根据当前配置以交互方式可视化 Z-fighting。此工具使用 3 种深度测试渲染以 Z 轴为中心的两个四边形或平面。你可以使用键盘和鼠标滚轮以交互方式更改两个平面的 Z 坐标和对数深度的参数：

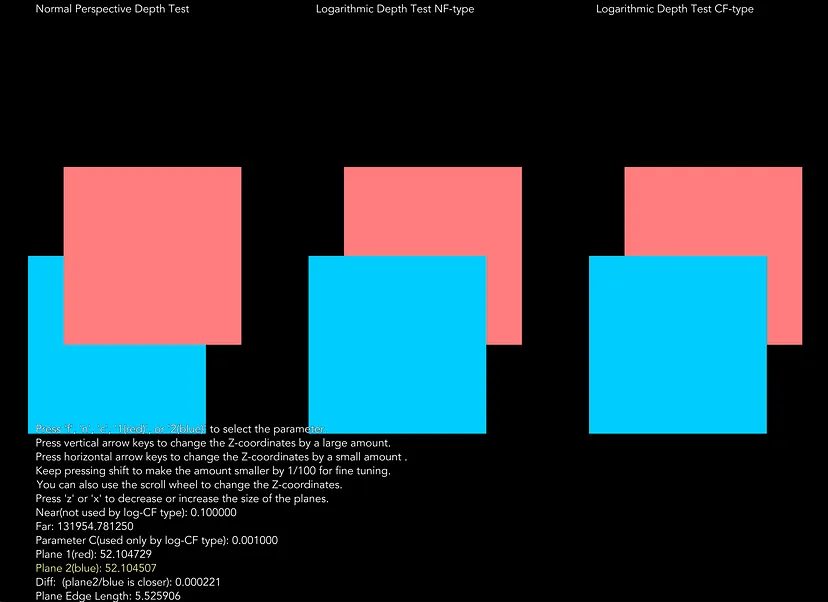
上图是该工具的快照，其参数设置如下：

• 平面 1（红色）放置在 z=-52.104729 处
• 平面 2（蓝色）放置在 z=-52.104507 处
• 远平面 = 131954.781250 / 近平面 = 0.1 / C = 0.001

如你所见，使用普通透视投影的深度测试失败，而两个对数深度测试成功。

7.2 depth_test_shader_comparator

此工具可视化了由改变的 gl_Position 引起的几何失真，其中对数深度分配给 Z 坐标。

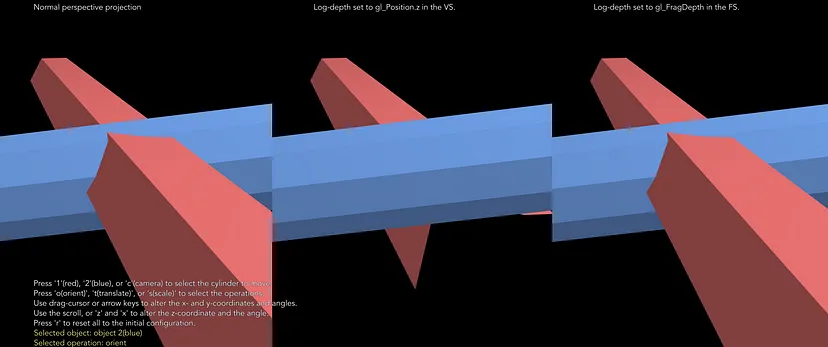
上图是该工具的快照。它渲染了两个圆柱形多面体的合成图。有三个窗格。左侧窗格使用普通透视深度测试进行渲染。中间窗格使用 NF 类型的对数深度进行渲染，深度值在顶点着色器中分配给 gl_Position。右侧窗格使用 NF 类型进行渲染，但值在片段着色器中分配给 gl_FragDepth。如你所见，中间窗格的渲染存在不正确的遮挡，并且红色多面体的几何形状明显扭曲。

你可以交互地更改以下参数，并实时查看效果：

• 圆柱形多面体的长度和半径。
• 圆柱形多面体的位置和方向
• 相机的位置和方向。

7.3 depth_test_batch

这是一个命令行批处理测试器，通过使用 OpenGL 将渲染四边形实际运行到帧缓冲区来查找最小间隙。对于 VCS 中沿负 Z 轴的每个点 Z_vcs，它通过结合网格搜索和二分搜索来找到两个平面之间的最小间隙 Δz。为了减轻误报的影响，它会执行多次测试（数量由命令行参数 -num_perturbed_samples指定）。对于每次测试，都会向平面的 Z 坐标添加小的随机扰动。如果所有测试都成功，则认为 Z-vcs 和 Δz 通过。

该工具采用以下参数。

• -depth_type <perspective/logfn/logcf>
• -near <near(positive)>
• -far <far(positive)>
• -c <CF 类型的参数 C>
• -num_points
• -num_perturbed_samples

然后，该工具对 VCS 中的 Z 坐标或 Z_vcs 进行 Δz 采样。`Z_vcs` 的数值由参数 -num_points给出，这些点以对数形式均匀分布在 -near 和 -far 之间比例。结果将打印到标准错误输出。

以下是上述图表所用命令的示例调用：

./depth_test_batch -depth_type perspective -near 1.0e-1 -far 1.0e10 -c 1.0 -num_points 100 -num_perturbed_samples 5

8、结束语

这篇博文涵盖了在实际使用中处理 Z-fighting 的要点。处理它最省心的方法是使用 NF 类型的对数深度和 gl_FragDepth。它应该涵盖大多数用例。如果它不能满足你的性能要求，那么你可以使用其他方法，但你应该意识到缺点。无论哪种方式，我希望这篇文章和工具能够帮助你分析 Z-fighting 的问题，并在你必须应对它时做出更好的决策。

原文链接：Practical Analysis on the Z-fighting and the Logarithmic Depth Tests for Computer Graphics

BimAnt翻译整理，转载请标明出处