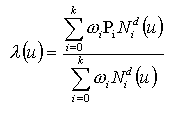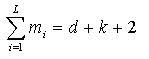IfcBSplineCurve
Definition from ISO/CD 10303-42:1992: A B-spline curve is a
piecewise parametric polynominal or rational curve described in terms of
control points and basis functions. The B-spline curve has been selected as the
most stable format to represent all types of polynominal or rational parametric
curves. With appropriate attribute values it is capable of representing single
span or spline curves of explicit polynomial, rational, Bezier or B-spline
type.
Interpretation of the data is as follows:
-
All weights shall be positive and the curve is given by
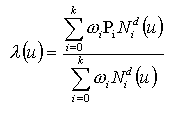
| k+1 |
= number of control points |
| Pi |
= control points |
| wi |
= weights |
| d |
= degree |
The knot array is an array of (k+d+2) real numbers
[u-d ... uk+1], such that for
all indices j in [-d,k], uj <=
uj+1. This array is obtained from the knot data list by
repeating each multiple knot according to the multiplicity. N
di, the ith normalised B-spline basis function
of degree d, is defined on the subset [ui-d, ... ,
ui+1] of this array.
-
Let L denote the number of distinct values amongst the
d+k+2 knots in the knot array; L will be referred to as
the 'upper index on knots'. Let mj denote the multiplicity
(i.e. number of repetitions) of the jth distinct knot. Then
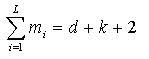
All knot multiplicities except the first and the last shall be in
the range 1 ... degree; the first and last may have a maximum value of degree +
1. In evaluating the basis functions, a knot u of e.g. multiplicity 3 is
interpreted as a string u, u, u, in the knot array. The B-spline curve
has 3 special subtypes (IAI note: only 1, Bezier curve, included in this IFC
release) where the knots and knot multiplicities are derived to provide
simple default capabilities.
- Logical flag is provided to indicate whether the curve self
intersects or not.
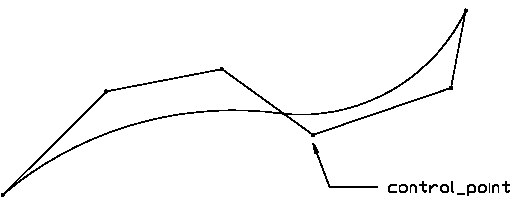
Illustration from ISO 10303-42:
NOTE: Corresponding STEP entity:
b_spline_curve. Please refer to ISO/IS 10303-42:1994, p. 45 for the final
definition of the formal standard.
HISTORY: New entity in Release IFC2x
Edition 2.
EXPRESS specification:
|
|
|
|
|
|
| ControlPoints
|
:
|
ARRAY [0:255] OF IfcCartesianPoint := IfcListToArray(ControlPointsList,0,UpperIndexOnControlPoints);
|
| UpperIndexOnControlPoints
|
:
|
INTEGER := (SIZEOF(ControlPointsList) - 1);
|
|
|
|
| WR41
|
:
|
SIZEOF(QUERY(Temp <* ControlPointsList |
Temp.Dim <> ControlPointsList[1].Dim))
= 0;
|
|
|
|
Attribute definitions:
| Degree
|
:
|
The algebraic degree of the basis functions.
|
| ControlPointsList
|
:
|
The list of control points for the curve.
|
| CurveForm
|
:
|
Used to identify particular types of curve; it is for information only.
|
| ClosedCurve
|
:
|
Indication of whether the curve is closed; it is for information only.
|
| SelfIntersect
|
:
|
Indication whether the curve self-intersects or not; it is for information only.
|
| ControlPoints
|
:
|
The array of control points used to define the geometry of the curve. This is derived from the list of
control points.
|
| UpperIndexOnControlPoints
|
:
|
The upper index on the array of control points; the lower index is 0.
This value is derived from the control points list.
|
Formal Propositions:
| WR41
|
:
|
All control points shall have the same dimensionality.
|
Inheritance graph
|
|
|
|
|
|
| ControlPoints
|
:
|
ARRAY [0:255] OF IfcCartesianPoint := IfcListToArray(ControlPointsList,0,UpperIndexOnControlPoints);
|
| UpperIndexOnControlPoints
|
:
|
INTEGER := (SIZEOF(ControlPointsList) - 1);
|
|
|
|