
IfcEdge
Definition from ISO/CD 10303-42:1992: An edge is the topological
construct corresponding to the connection of two vertices. More abstractly, it
may stand for a logical relationship between two vertices. The domain of an
edge, if present, is a finite,
non-self-intersecting open curve in RM, that is, a connected
1-dimensional manifold. The bounds of an edge are two vertices, which need not
be distinct. The edge is oriented by choosing its traversal direction to run
from the first to the second vertex. If the two vertices are the same, the edge
is a self loop. The domain of the edge does not include its bounds, and 0 ≤
Ξ ≤ ∞. Associated with an edge may be a geometric curve to locate
the edge in a coordinate space; this is represented by the edge curve
(IfcEdgeCurve) subtype. The curve shall be finite and non-self-intersecting
within the domain of the edge. An edge is a graph, so its multiplicity M and
graph genus Ge may be determined by the graph traversal
algorithm. Since M = E = 1, the Euler equation (1) reduces in the
case to
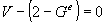
where V = 1 or 2, and Ge = 1 or 0.
Specifically, the topological edge defining data shall satisfy:
- - an edge has two vertices
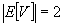
- - the vertices need not be distinct
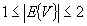
- - Equation (2) shall hold.
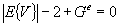
NOTE
Corresponding STEP entity: edge. Please refer to ISO/IS 10303-42:1994, p. 130
for the final definition of the formal standard.
HISTORY New Entity in IFC Release 2.0
Informal propositions:
- The edge has dimensionality 1.
- The extend of an edge shall be finite and nonzero
EXPRESS specification:
Attribute definitions:
| EdgeStart
|
:
|
Start point (vertex) of the edge.
|
| EdgeEnd
|
:
|
End point (vertex) of the edge. The same vertex can be used for both EdgeStart and EdgeEnd.
|
Inheritance graph
![]()